SOLUTION: A, B and C are distinct digits and 4 * AB = CA. Find the sum A+B+C

Since  4 * AB = CA,  CA must be a two-digit number >= 40.    (*)


Since  4 * AB = CA,  we conclude that AB is a two-digit number between 10 and 24, inclusive.


So, A is either 1 or 2.  But from 4 * AB = CA, digit A must be even - so,
we conclude that A = 2.


Thus, CA is a two digit number multiple of 4 and with the last digit 2.


Such numbers CA can be only 12, 32, 52, 72, 92.

Condition (*) prohibits 12 and 32, so the remaining opportunities for CA are 52, 72, 92.


Divide CA by 4, and you will get the values  13, 18, 23  for AB.


But, as we established above, the digit A is 2;  therefore,  AB can only be 23.


Thus, A = 2;  B = 3;  C = 9.  All these digits are different.


The sum  A + B + C is  2 + 3 + 9 = 14.    ANSWER

A, B and C are distinct digits and 4 * AB = CA. Find the sum A+B+C

4AB = CA
Obviously, AB and CA are 2-digit numbers
As such. AB = 10A + B, and CA = 10C + A. So, 4AB = CA becomes:
4(10A + B) = 10C + A	
40A + 4B = 10C + A	
4B = 10C + A - 40A	
4B = 10C - 39A	
B =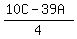 
Now, we can see that C - 39A is a MULTIPLE of 4, so A CANNOT be an ODD DIGIT. Furthermore, the digit A MUST be less than 3,
as ANY digit greater than 3 would yield a negative (< 0) numerator. And, neither can digit A be 0 because, while the units
digit in CA can be 0, the tens digit in AB CANNOT.

Having said that, digit A being less than 3, not ODD, and NOT 0 makes it 2
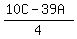B = 
B = 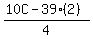 ----- Substituting 2 for A
B = 
At this point, 10C MUST be greater than 78, which means that C can be 8 or 9. But, if C = 8, then numerator becomes 2, and 2 is
NOT a MULTIPLE of 4. So, C MUST be 9
B = 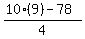 ------ Substituting 9 for C
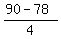B = 
B = 
B = 3	
Therefore, (A, B, C) = (2, 3, 9), and A + B + C = 2 + 3 + 9 = 14	

You can do the CHECK!!