Question 1209417: Some prime numbers are of the form  . For example, the prime number 7 is equal to 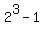 . Make a list of the first seven exponents (n<20) that produce prime numbers of this type (include the number 3 as one of the seven in your list).
CC11F #5
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Some prime numbers are of the form . For example, the prime number 7 is equal to .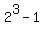
Make a list of the first seven exponents (n<20) that produce prime numbers of this type
(include the number 3 as one of the seven in your list).
CC11F #5
~~~~~~~~~~~~~~~~~~~~~~~~~~~
ANSWER. The first seven exponents n < 20 that produce prime numbers of the form are 2, 3, 5, 7, 13, 17, and 19.
For the solution, see the link
https://www.google.com/search?q=.+Some+prime+numbers+are+of+the+form+%7B%7B%7B2%5En-1%7D%7D%7D.+For+example%2C+the+prime+number+7+is+equal+to+%7B%7B%7B2%5E3-1%7D%7D%7D.+Make+a+list+of+the+first+seven+exponents+(n%3C20)+that+produce+prime+numbers+of+this+type+(include+the+number+3+as+one+of+the+seven+in+your+list).+CC11F+%235&rlz=1C1CHBF_enUS1071US1071&oq=.+Some+prime+numbers+are+of+the+form+%7B%7B%7B2%5En-1%7D%7D%7D.+For+example%2C+the+prime+number+7+is+equal+to+%7B%7B%7B2%5E3-1%7D%7D%7D.++Make+a+list+of+the+first+seven+exponents+(n%3C20)+that+produce+prime+numbers+of+this+type++(include+the+number+3+as+one+of+the+seven+in+your+list).+CC11F+%235&gs_lcrp=EgZjaHJvbWUyBggAEEUYOdIBCTQwNjdqMGoxNagCCLACAQ&sourceid=chrome&ie=UTF-8
This solution is provided by artificial intelligence (AI) by my request.
Among the obvious facts that are useful to know, in order for be
a prime integer number, the exponents n must be an odd integer number.
The even exponents n, higher than 2, produce composite numbers.
Among other useful facts to know is THIS:
if the exponent n is a composite number,
then is a composite number, too.
So, for such a search as in this problem, you should look among prime exponents n,
rejecting composite exponents n.
Enjoy (!)
|
|
|
