Question 1209411: Find all solutions of the equation |x^2 - 30x - 1| = 30 + |6x - 2| + |x^2 - 20x - 4|.
Found 3 solutions by Edwin McCravy, KMST, ikleyn:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Before graphing calculators, it would have been a more complicated
The right hand is greater than 30 except for all values of 
 for all of real values because for all of real values because
 for all real numbers, for all real numbers,
with  for for  , and , and  otherwise. otherwise.
 for for
 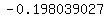 and and  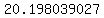 . .
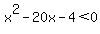 and and 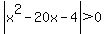 for for
for  such that such that 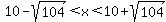
For the left hand side,  , has as solutions , has as solutions 
For values of  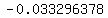 and and  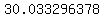 , ,
 and and  . .
For 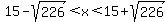 
Those limiting values are approximately 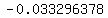 and and 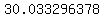 . .
For  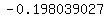 , , 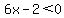 , while , while 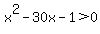 and and 
and the equation turns into


 --> --> 
For 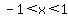 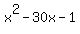 is decreasing from is decreasing from  at at  to a minimum 0f to a minimum 0f  at at  and then increasing to and then increasing to  at at  and and 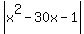 is less than the value of is less than the value of 
=
For  , ,  , ,  , and , and 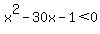 , ,
so  and and 
The equation turns into


 --> --> 
For 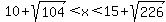  while while
 and and 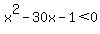 , so , so 
turning the equation into 

 --> --> 
 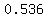 does not comply with does not comply with 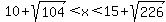
 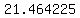 is a solution between is a solution between  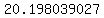 and and  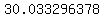
For   , ,  , and , and  , ,
turning the equation into 

 --> -->  is not a solution complying with is not a solution complying with  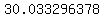
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For problems like this one, there is a standard methodology/strategy for solving.
You should subdivide the number line by sections (= intervals).
The division point are the points where the participating functions under absolute values
(parts of the equation) change their signs.
Then for each interval, from minus infinity to infinity, you write an equation
using each function with its native sign as it should be, dictated by the absolute
value rule at this interval.
Then you solve the updated equation and check if the solution does belong to this particular
interval under the consideration.
If the particular solution does belong to this particular interval, then the found solution
is the solution to the original equation.
If it does not belong, then the found solution is not a solution to the original equation.
As you complete going from the left  to the right to the right  , you complete the solution. , you complete the solution.
The rest is just a technique and the arithmetic.
I think, if a student does understand it and demonstrates his/her understanding, it should be just
enough for the teacher to accept the assignment.
As the problem is twisted in this post, it is twisted TOO much and teaches nothing.
A teacher who assigns such tasks, should be checked for adequacy.
|
|
|