SOLUTION: How many pairs of integers (a,b) satisfy the equation {{{ab^a}}} = 648? CC11F #10

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: How many pairs of integers (a,b) satisfy the equation {{{ab^a}}} = 648? CC11F #10      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1209405: How many pairs of integers (a,b) satisfy the equation 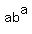ab%5Ea = 648?
CC11F #10
Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


ab%5Ea=648=%282%5E3%29%283%5E4%29

The only prime factors of 648 are 2 and 3.

a is an exponent in the expression; the exponents in the prime factorization of 648 are 3 and 4. That means a can only be 1, 2, or 3.

(1) a=1

%281%29%28b%5E1%29=648
b=648

first solution: (a,b) = (1,648)

(2) a=2

%282%29%28b%5E2%29=648
b%5E2=648%2F2=324
b=18 or b=-18

second and third solutions: (a,b) = (2,18) and (a,b) = (2,-18)

(3) a=3

%283%29%28b%5E3%29=648
b%5E3=216
b=6

fourth solution: (a,b) = (3,6)

ANSWER: 4 pairs of integer (a,b) satisfy the equation ab^a = 648