|
Question 1209290: Solve the inequality x(x + 6) > 16 - x^2 + 14x. Write your answer in interval notation.
Found 2 solutions by mccravyedwin, math_tutor2020:
Answer by mccravyedwin(408)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Consider the equation 
Let's get everything to one side.






That last equation is of the format 
where,
a = 1, b = -4, c = -8
Plug those into the quadratic formula.









 or or 
 or or  both of which are approximate. both of which are approximate.
--------------------------------------------------------------------------
Draw a number line with regions A, B, C
region A = stuff to the left of -1.464
region B = stuff between -1.464 and 5.464
region C = stuff to the right of 5.464
Possible test values for regions A,B,C could be: x = -2, x = 0, x = 6 in that order
You plug each test value back into the original inequality 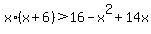 to see if we get a true statement or not. to see if we get a true statement or not.
If we tried x = -2, then,
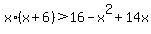
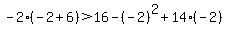
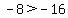
which is true.
Any x value in region A is in the solution set for 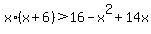
Region A is  aka aka 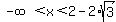
Yielding the interval notation 
Use curved parenthesis to indicate we do not include the endpoints in the solution set.
If we tried x = 0 then
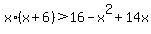
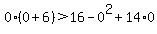

which is false.
Any x value in region B, ie the region between  and and  will make the original inequality false. will make the original inequality false.
The last region to test is region C.
Let's plug in x = 6
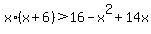
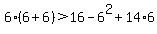
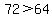
which is true
Therefore 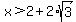 aka aka 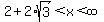 translates to the interval notation translates to the interval notation 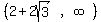
We found these two interval notation regions
 or or 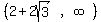
Glue them together with a set union symbol to end up with this final answer

You can use a graphing calculator like Desmos and GeoGebra to confirm.
|
|
|
| |