SOLUTION: The radical {{{sqrt((80)+sqrt(1776))}}} can be expressed as {{{sqrt(a) +sqrt(b)}}}, where a < b. What is the product "ab"?

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: The radical {{{sqrt((80)+sqrt(1776))}}} can be expressed as {{{sqrt(a) +sqrt(b)}}}, where a < b. What is the product "ab"?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1209214: The radical sqrt%28%2880%29%2Bsqrt%281776%29%29 can be expressed as sqrt%28a%29+%2Bsqrt%28b%29, where a < b. What is the product "ab"?
Found 3 solutions by math_tutor2020, ikleyn, greenestamps:
Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Answer: 444

Explanation
I'll assume that a,b are positive integers.

sqrt%2880%2Bsqrt%281776%29%29=sqrt%28a%29+%2Bsqrt%28b%29

%28sqrt%2880%2Bsqrt%281776%29%29%29%5E2=%28sqrt%28a%29+%2Bsqrt%28b%29%29%5E2 Square both sides



80%2Bsqrt%281776%29=a%2B2%2Asqrt%28ab%29%2Bb

80%2Bsqrt%281776%29=%28a%2Bb%29%2B2%2Asqrt%28ab%29

Notice these matching pairs on either side

The red and green boxes indicate that a%2Bb+=+80 and 2%2Asqrt%28ab%29+=+sqrt%281776%29

Rewrite the 2nd equation like so
2%2Asqrt%28ab%29+=+sqrt%281776%29

%282%2Asqrt%28ab%29%29%5E2+=+%28sqrt%281776%29%29%5E2

4ab+=+1776

ab+=+1776%2F4

ab+=+444


Extra info:
Solving the system system%28a%2Bb+=+80%2C+2%2Asqrt%28ab%29+=+sqrt%281776%29%29 leads to (a,b) = (6,74) when considering a < b
a+b = 6+74 = 80
a*b = 6*74 = 444
sqrt%2880%2Bsqrt%281776%29%29=sqrt%286%29+%2Bsqrt%2874%29

Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
The radical sqrt%28%2880%29%2Bsqrt%281776%29%29 can be expressed as sqrt%28a%29+%2Bsqrt%28b%29, where a < b. What is the product "ab"?
~~~~~~~~~~~~~~~~~~


This problem is posed INCORRECTLY.

It gives one equation for two variables, "a" and "b", and asks about the value of the product "ab".

This equation has INFINITELY MANY possible solutions for "a" and "b", and,
respectively, there are INFINITELY MANY different possible values of "ab".


Nevertheless, the other tutor deduces the unique value as the answer.

Why ? - Because his solution is erroneous: it has an error. 

The other tutor deduces this equation

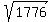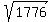    80 + sqrt%281776%29 = {(a+b) + 2%2Asqrt%28ab%29.    (1)


Till this point, everything is correct.


But in the next step, the other tutor concludes that from this equation, we have 

    80 = a + b,  sqrt%281776%29 = 2%2Asqrt%28ab%29.    (2)


and continues with it.


This step is an error. There is / (there are) no logical deducing from (1) to (2).

Making this logical deducing is the error.


Again, the given / (original) equation has infinitely many solutions in real numbers,
and they create infinitely many possible values for "ab".


If somebody wants to create a correct problem from this, the problem's formulation must be changed:
more restrictions to "a" and "b" should be imposed.



Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


Consider the following calculation, using the pattern x%2By%29%5E2=x%5E2%2B2xy%2By%5E2:

%28sqrt%28a%29%2Bsqrt%28b%29%29%5E2=a%2B2sqrt%28ab%29%2Bb=%28a%2Bb%29%2B2sqrt%28ab%29

To evaluate the given expression, put the expression in the radical in the form above by extracting sqrt%284%29=2 from the radical:

sqrt%28%2880%29%2Bsqrt%281776%29%29=sqrt%28%2880%29%2B2sqrt%28444%29%29

The problem is now finished by finding a and b such that (a+b)=80 and ab=444.

Solve that pair of equations to find the answer, remembering that the problem specifies a < b.

a%2Bb+=+80
b+=+80-a
ab+=+a%2880-a%29=444
80a-a%5E2=444=0
a%5E2-80a%2B444=0

Note that to solve this by factoring (without using the quadratic formula), we need to find two numbers whose product is 444 and whose sum is 80. That is what the original problem requires us to do, so the formal algebra doesn't get us any closer to the answer.

So use logical trial and error to find the two numbers are 74 and 6: 74+6 = 80 and 74*6 = 444.

Then, since a is the smaller of the two numbers....

ANSWER: a = 6, b = 74; sqrt%28%2880%29%2Bsqrt%281776%29%29=sqrt%286%29%2Bsqrt%2874%29