SOLUTION: If {{{ab^2c^4=2430000}}}, where a, b and c are distinct positive integers greater than 1, What is the greatest possible value of a+b+c?

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: If {{{ab^2c^4=2430000}}}, where a, b and c are distinct positive integers greater than 1, What is the greatest possible value of a+b+c?       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1209213: If ab%5E2c%5E4=2430000, where a, b and c are distinct positive integers greater than 1, What is the greatest possible value of a+b+c?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


Tutor @ikleyn has pointed out that I lost track of what I was doing in my original response. Following is my corrected solution.



In the given algebraic expression, the exponent on a is odd and the exponents on b and c are even; in the factored form of the constant, the exponent on the factor 3 is odd and the exponents on the factors 2 and 5 are even. That means a must be 3^5=243.

That leaves us with

%28b%5E2%29%28c%5E4%29=%282%5E4%29%285%5E4%29

Since a, b, and c are each greater than 1, there are two possibilities:
(1) b%5E2=2%5E4 and c%5E4=5%5E4, which gives us b=2%5E2=4 and c=5
(2) b%5E2=5%5E4 and c%5E4=2%5E4, which gives us b=5%5E2=25 and c=2

For case (1), a+b+c = 243+4+5 = 252; for case (2), a+b+c = 243+25+2 = 270.

ANSWER: 270

Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
If ab%5E2c%5E4=2430000, where a, b and c are distinct positive integers greater than 1,
What is the greatest possible value of a+b+c?
~~~~~~~~~~~~~~~~~~~~~~~~~~ 


2430000 = 3^5 * 2^4 * 5^4.


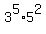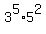Arrange the factors this way  a = 3%5E5%2A5%5E2,  b = 5,  c = 2.


Then a + b + c = 3%5E5%2A5%5E2 + 5 + 2 = 6075 + 5 + 2 = 6082.    ANSWER

---------------------

This problem is a  TRAP.

It requires attention and accuracy.   Also,  there is a guiding  highlight%28highlight%28IDEA%29%29,  which leads to correct solution.

The  IDEA  is  THIS:

    Load as much as possible to factors with lower degrees.


        Then these factors with lower degrees, loaded as much as possible,
        will contribute a lot and will provide the maximum of the sum a + b + c.


/\/\/\/\/\/\/\/\/


On my way to correct solution, I changed my writing in this post several times.

Sorry for this, but it was my way to the truth.

Finally, I got the correct solution.