Question 1209212: Simplify the following equation in the image:
https://ibb.co/5K1GC71
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Simplify the following  expression in the image: expression in the image:
https://ibb.co/5K1GC71
~~~~~~~~~~~~~~~~~~~~~~~~~~
I made my editing in this post, because THERE IS NO equation in it.
There is an expression, instead, which should be simplified / evaluated.
The starting expression is
S = 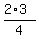 + + 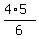 + + 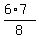 + . . . + + . . . + 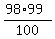 - ( - ( + +  + +  + . . . + + . . . +  ).
it can be re-grouped as the sum of addends ).
it can be re-grouped as the sum of addends
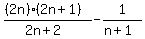 , n = 1, 2, 3, . . . , 49.
Each addend can be simplified , n = 1, 2, 3, . . . , 49.
Each addend can be simplified
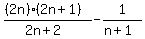 = = 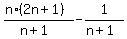 = 2n-1.
So, the original sum is the sum of the terms (2n-1), n= 1, 2, 3, . . . 49
1 + 3 + 5 + . . . + 97.
It is the sum of an arithmetic progression with the first term = 2n-1.
So, the original sum is the sum of the terms (2n-1), n= 1, 2, 3, . . . 49
1 + 3 + 5 + . . . + 97.
It is the sum of an arithmetic progression with the first term  = 1, last term = 1, last term  = 97 and the number of terms = 97 and the number of terms  + 1 = 49.
The sum of this progression is
S = + 1 = 49.
The sum of this progression is
S = 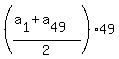 = = 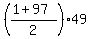 = =  = 2401.
ANSWER. The given expression has the value of 2401. = 2401.
ANSWER. The given expression has the value of 2401.
Solved.
|
|
|