Question 1209198: Hi
It took a train 65 seconds from starting to cross an iron bridge of length 1440m to completely pass over the bridge. It also took the train 75 seconds from when it entered a 1680m tunnel to completely pass through the tunnel.
Find the length and speed of the train.
Found 3 solutions by ikleyn, math_tutor2020, mananth:
Answer by ikleyn(52864)   (Show Source):
You can put this solution on YOUR website! .
It took a train 65 seconds from starting to cross an iron bridge of length 1440 m
to completely pass over the bridge.
It also took the train 75 seconds from when it entered a 1680m tunnel to completely
pass through the tunnel.
Find the length and speed of the train.
~~~~~~~~~~~~~~~~~~~~~
Let L be the length of the train (in meters),
and let V be the speed of the train, in meters per second.
For passing the bridge, we have this equation
L + 1440 = 65*V. (1)
For passing the tunnel, we have this equation
L + 1680 = 75*V. (2)
Subtract equation (1) from equation (2). You will get
1680 - 1440 = 75V - 65V,
240 = 10V
V = 240/10 = 24.
The train speed is 24 m/s, or 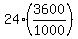 = 86.4 kilometers per hour.
The length of the train, from equation (1), is
L = 65*24 - 1440 = 120 meters.
Solved.
I appreciate the fact that the input numbers are reasonable.
My great congratulations to the problem's composer.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
Answers:
Length = 120 meters
Speed = 86.4 kilometers per hour (equivalent to 24 meters per second)
Explanation:
L = length of the train
When the tip of the train engine is just starting to cross the bridge, the back-most part of the caboose is L meters away from the start of the bridge.
The caboose must travel this distance L, plus the length of the bridge, so that the entire train is off the bridge.
It might be useful to make a number line drawing.
The caboose travels L+1440 meters in 65 seconds.
distance = rate*time
rate = distance/time
rate = (L+1440 meters)/(65 seconds)
rate = (L+1440)/(65) meters per second
Using similar logic, we find that the rate can also be written as (L+1680)/75 when considering the tunnel scenario.
Those two rates are assumed to be equal since we assume the train doesn't speed up nor slow down when on the bridge vs tunnel.
bridge speed = tunnel speed
(L+1440)/65 = (L+1680)/75
75(L+1440) = 65(L+1680)
75L+108000 = 65L+109200
75L-65L = 109200-108000
10L = 1200
L = 1200/10
L = 120
The train is 120 meters long.
Then we use that length to find the train's speed
bridge speed = (L+1440)/65
bridge speed = (120+1440)/65
bridge speed = 24 meters per second
or,
tunnel speed = (L+1680)/75
tunnel speed = (120+1680)/75
tunnel speed = 24 meters per second
We get the same speed either way.
You only need to show scratch work on one set rather than both.
However, showing that both lead to the same speed helps confirm we got the correct length.
To convert from "meters per second" to "kilometers per hour", you could have this scratch work.
Note that 1 hour = 60*60 = 3600 seconds.
We see that 24 meters per second = 86.4 kilometers per hour.
Each multiplier fraction is set up so that the "meters" and "seconds" units cancel.
The result 86.4 is exact and hasn't been rounded.
Answer by mananth(16946)  (Show Source):
You can put this solution on YOUR website! it took a train 65 seconds from starting to cross an iron bridge of length 1440m to completely pass over the bridge. It also took the train 75 seconds from when it entered a 1680m tunnel to completely pass through the tunnel.
Find the length Letand speed of the train.
Let speed of train be x m
Let length of train be y m
Length of bridge be 1440 s
distance to cover = (y+1440)
time =65 s
65 = (y+1440)/x
65x = y+1440
65x-1440 =y..................1
For the other bridge
75 = (y+1680)/x
75x = y+1680
y= 75x -1680.............2
Equate both equations
75x-1680 = 65x - 1440
Rearrange
75x-65x = 1680-1440
10x = 240
x =24 m/s
Speed of train = 24m/s
Plug value of x in 65x-1440 =y
65*24 -1440 = y
y=120 m
Length of train is 120 m
|
|
|
