SOLUTION: what is the range of (fxg): f(x)=2x^2+3 g(x)=1/x

The function (fxg)(x) is F(x) =  = 2x + .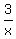


They ask about the range of this function.


The plot is shown in this link  

    https://www.desmos.com/calculator/lh7qjcdhic 

    https://www.desmos.com/calculator/lh7qjcdhic



There are two ways to solve this problem: one way is Algebra, and another way is Calculus.


              Algebra way


The range is the set of real values t such that

    2x + 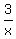 = t  for some x.


In other words, the range is the set of real numbers t such that the quadratic equation

    2x^2 + 3 = tx,  or  2x^2 - tx + 3 = 0  

has real solutions for x.


For it, the necessary and sufficient condition is that the discriminant is non-negative

    d = (-t)^2 - 4*2*3 >= 0,  or  t^2 >= 24,   or  |t| >= ,  or


          +------------------------------------+
          |    t <= 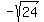   or  t >= .   |
          +------------------------------------+


Thus the range of the function  (fxg)  is the union of the two sets  


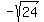    (,] U [,).    ANSWER