Question 1209153: If f(x)= (k+x³sec(x))/(sin(b)×(x-π)) is continuous at x= π, and kb -f(π)= 4(π^(5/ 2) , find the value of b .
Found 4 solutions by ikleyn, Edwin McCravy, mccravyedwin, AnlytcPhil:
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If f(x)= (k+x³sec(x))/(sin(b)×(x-π)) is continuous at x= π,
and kb -f(π)= 4(π^(5/ 2) , find the value of b .
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In the last equation, in its right side, there are two opening parentheses and
only one closing parenthesis.
So, formally speaking, this equation is written incorrectly.
Double check your post.
/////////////////////////////
I think that the Edwin' solution is not adequate to the problem,
so I bring here another solution.
sec(x) = 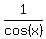 .
When x approaches to π, then cos(x) approaches to -1; hence, sec(x) approaches to -1.
It means that k+x^3*sec(x) in the numerator is close to k-x^3.
In the denominator, sin(b) is a non-zero constant, so, we should not worry about it.
But in the denominator, we have x-π, and, in order for the expression be a continuous function,
k-x^3 in the numerator must put out this x-π in the denominator.
Hence, k must be π^3. Then the numerator, as x approaches to π, is equivalent
to π^3-x^3 = (π-x)*(π^2 +πx + x^2), and it puts out x-π in the denominator.
So, we deduced logically that the expression is a continuous function if and only if k = π^3.
Then kb = .
When x approaches to π, then cos(x) approaches to -1; hence, sec(x) approaches to -1.
It means that k+x^3*sec(x) in the numerator is close to k-x^3.
In the denominator, sin(b) is a non-zero constant, so, we should not worry about it.
But in the denominator, we have x-π, and, in order for the expression be a continuous function,
k-x^3 in the numerator must put out this x-π in the denominator.
Hence, k must be π^3. Then the numerator, as x approaches to π, is equivalent
to π^3-x^3 = (π-x)*(π^2 +πx + x^2), and it puts out x-π in the denominator.
So, we deduced logically that the expression is a continuous function if and only if k = π^3.
Then kb =  ,
f(π) = - ,
f(π) = - 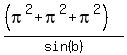 = - = - 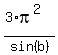 ;
and kb - f(π) = ;
and kb - f(π) =  + + 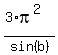 .
It gives us this equation .
It gives us this equation
 + + 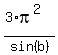 = 4*pi^(5/2).
and we want to solve it for "b". Divide all the terms by = 4*pi^(5/2).
and we want to solve it for "b". Divide all the terms by 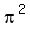 to get to get
 + + 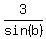 = = 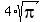 .
This equation is not algebraic and can not be solved using algebraic methods.
So, solve it numerically/graphically.
I used online graphical solver www.desmos.com/calculator
(free of charge online solver for common use).
See the plot and the numbers in it under this link
https://www.desmos.com/calculator/20kerz6s92
https://www.desmos.com/calculator/20kerz6s92
ANSWER. As you can see from the plot, there are many different possible solutions for "b".
They are x-coordinates of intersections of the curves with the horizontal straight line.
There are positive and negative solutions. Of them, the minimal positive value of "b" is 0.62526 (approximate). .
This equation is not algebraic and can not be solved using algebraic methods.
So, solve it numerically/graphically.
I used online graphical solver www.desmos.com/calculator
(free of charge online solver for common use).
See the plot and the numbers in it under this link
https://www.desmos.com/calculator/20kerz6s92
https://www.desmos.com/calculator/20kerz6s92
ANSWER. As you can see from the plot, there are many different possible solutions for "b".
They are x-coordinates of intersections of the curves with the horizontal straight line.
There are positive and negative solutions. Of them, the minimal positive value of "b" is 0.62526 (approximate).
Solved.
=======================
Here I will explain WHY I said that the solution by Edwin is inadequate.
The condition of continuity for function f(x) at x =  is given in the problem is given in the problem
in order for the person, who solves it, would determine the value of "k" from this condition.
I did it and determined that the value of "k" must be 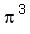 . .
Thus I determined one of the two unknown variables in the problem, namely "k";
after that, variable "b" remained as the single variable and the only variable to find.
Edwin in his solution didn’t notice, at all, that variable "k" can be determined
and should be determined from this condition, so it remained undefined until
the very end in his solution.
\\\\\\\\\\\\\\\\\\\\\\\\\\\
To those visitors, who want to know HOW TO to pose this kind of problems
in a right way and to solve them intelligently, I recommend to look into my lesson
- Couple of non-standard Calculus problems
in this site and read Problem 2 from there.
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
Answer by mccravyedwin(409)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here are a couple of videos on L'Hopital's theorem for you:
The undefined indeterminate forms are  https://www.youtube.com/watch?v=Gh48aOvWcxw
https://www.youtube.com/watch?v=g45quDrSA6g
Edwin
https://www.youtube.com/watch?v=Gh48aOvWcxw
https://www.youtube.com/watch?v=g45quDrSA6g
Edwin
Answer by AnlytcPhil(1810)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn took the denominator as
(sin(b)×(x-π)), as it was typed.
However, I purposely changed it to
(sin(b(x-π)).
She tried to solve this problem using f(x) as it was written:
  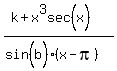 and found that it was unsolvable for b by ordinary mathematical means.
However, I assumed the student had mistyped, and that f(x) should have been
this instead:
and found that it was unsolvable for b by ordinary mathematical means.
However, I assumed the student had mistyped, and that f(x) should have been
this instead:
   By making this change, I was able to solve for b using the quadratic formula.
Why did I assume that the student has mistyped?
I reasoned that no professional math problem-creator would have included
only one sine function of a constant, in this case, sin(b). If a professional
problem-creator included a sine function, they certainly would have used a sine
function of a VARIABLE, not the sine of a CONSTANT, which would be a constant
itself! So I changed the denominator so that the sine function would be of a
variable, not of a constant.
Also, no professional math problem-creator would create a problem that would
not be solvable by ordinary means taught in normal calculus courses.
So I changed the denominator (sin(b)×(x-π)) to (sin(b(x-π)) and was able to
solve for b using the quadratic formula.
It made more sense to me that a typo had been made, rather than an incompetent
math-problem-creator -- especially since there was a typo of a missing right
parenthesis in this:
4(π^(5/ 2
which Ikleyn mentioned.
Also, when a problem contains k, this letter is nearly always taken as an
arbitrary constant, but Ikleyn found k not to be arbitrary at all.
I think my interpretation was the intended problem. Maybe Ikleyn will agree
with me on that.
Edwin
By making this change, I was able to solve for b using the quadratic formula.
Why did I assume that the student has mistyped?
I reasoned that no professional math problem-creator would have included
only one sine function of a constant, in this case, sin(b). If a professional
problem-creator included a sine function, they certainly would have used a sine
function of a VARIABLE, not the sine of a CONSTANT, which would be a constant
itself! So I changed the denominator so that the sine function would be of a
variable, not of a constant.
Also, no professional math problem-creator would create a problem that would
not be solvable by ordinary means taught in normal calculus courses.
So I changed the denominator (sin(b)×(x-π)) to (sin(b(x-π)) and was able to
solve for b using the quadratic formula.
It made more sense to me that a typo had been made, rather than an incompetent
math-problem-creator -- especially since there was a typo of a missing right
parenthesis in this:
4(π^(5/ 2
which Ikleyn mentioned.
Also, when a problem contains k, this letter is nearly always taken as an
arbitrary constant, but Ikleyn found k not to be arbitrary at all.
I think my interpretation was the intended problem. Maybe Ikleyn will agree
with me on that.
Edwin
|
|
|