Question 1209141: Carly just opened her own nail salon. Based on experience, she knows that her daily profit, P, in dollars, can be modelled by the relation P=-15x^2+240x-640, where x is number of clients per day. How many clients should she book each day to maximize her profit?
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Carly just opened her own nail salon. Based on experience, she knows that her daily profit, P,
in dollars, can be modelled by the relation P=-15x^2+240x-640, where x is number of clients
per day. How many clients should she book each day to maximize her profit?
~~~~~~~~~~~~~~~~~~~~
The given function is a quadratic function.
Since the coefficient at x^2 is negative, the parabola is downward and has a maximum.
The maximum value is achieved a 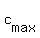 = =  , where "a" is the coefficient at x^2
and "b" is the coefficient at x. In your case, , where "a" is the coefficient at x^2
and "b" is the coefficient at x. In your case,
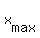 = = 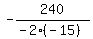 = = 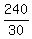 = 8.
Hence, the profit is maximum if Carly books 8 clients per day. ANSWER = 8.
Hence, the profit is maximum if Carly books 8 clients per day. ANSWER
Solved.
--------------------
On finding the maximum/minimum of a quadratic function see the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
Consider these lessons as your textbook, handbook, tutorials and (free of charge) home teacher.
Learn the subject from there once and for all.
|
|
|