Question 1209120: A teacher travels to work by either a bicycle or tricycle. There is probality of 2/7 that he travels by a tricycle on Monday. If he travels by a tricycle on any one day, there's a probability of 2/5 that he will travel by a bicycle the next day.If he by bicycle on every one day ,there is a probability of 5/9 that he will travel by tricycle the next day.Use a tree diagram to find the probability that he travels by a tricycle on Wednesday.
Answer by ikleyn(52852)   (Show Source):
You can put this solution on YOUR website! .
.
A teacher travels to work by either a bicycle or tricycle.
There is probability of 2/7 that he travels by a tricycle on Monday.
If he travels by a tricycle on any one day, there is a probability of 2/5 that he will travel by a bicycle the next day.
If he travels by a bicycle on every one day, there is a probability of 5/9 that he will travel by a tricycle the next day.
Use a tree diagram to find the probability that he travels by a tricycle on Wednesday.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Among different logical chains, we are interested with the chains that start on Monday
and finish by Wednesday/tricycle.
These chains, with their step-by-step probabilities, according to the problem, are
Monday/tricycle --> Tuesday/tricycle --> Wednesday/tricycle
2/7 3/5 3/5
Monday/tricycle --> Tuesday/bicycle --> Wednesday/tricycle
2/7 2/5 5/9
Monday/bicycle --> Tuesday/bicycle --> Wednesday/tricycle
5/7 4/9 5/9
Monday/bicycle --> Tuesday/tricycle --> Wednesday/tricycle
5/7 5/9 3/5
Now we can write for the desired probability
P(Wed/tri) =  .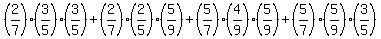
At this point, the substantive part of the solution ends - the rest is arithmetic.
Therefore, I will stop here, will put the formula into my calculator (which is MS Excel)
and give the ANSWER in the decimal form P = 0.5808 (rounded).
Solved.
Making a tree is an excessive and unnecessary job for me.
For me, this logical presentation in wording form is PREFERABLE.
|
|
|
