Question 1209118: Box A contains nine cards numbered 1 through 9, and box B contains five cards
numbered | through 5. A box is chosen at random and a card drawn; if the card shows
an even number, another card is drawn from the same box; if the card shows an odd
number, a card is drawn from the other box.
(i) What is the probability that both cards show odd numbers?
(ii) If both cards show odd numbers, what is the probability that they come from box B?
(iii) What is the probability that both cards show even numbers?
Answer by ikleyn(52832)   (Show Source):
You can put this solution on YOUR website! .
Box A contains nine cards numbered 1 through 9, and box B contains five cards
numbered  through 5. A box is chosen at random and a card drawn;
if the card shows an even number, another card is drawn from the same box;
if the card shows an odd number, a card is drawn from the other box.
(a) What is the probability that both cards show odd numbers?
(b) If both cards show odd numbers, what is the probability that they come from box B?
(c) What is the probability that both cards show even numbers?
~~~~~~~~~~~~~~~~~~~
(a) If both cards show odd numbers, it means, according to the problem, that
either first card is from box A, while second card is from box B
or (or exclusive) first card is from box B, while second card is from box A.
Therefore, P(a) =  +  =  = =  .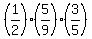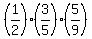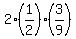
Here the factor  is the probability to choose randomly box A first or (exclusively) box B first.
(b) This probability is 0 (zero), since, by the meaning of the problem, this case is EXCLUDED/PROHIBITED.
(c) If both cards show even numbers, it means, according to the problem, that
either both cards are from box A or (or exclusive) both cards are from box B.
Therefore,
P(c) =  +  =  +  =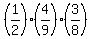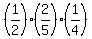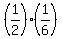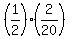
=  +  =  +  =  =  .
Again, here the factor is the probability to choose randomly box A first or (exclusively) box B first.
|
|
|
