SOLUTION: The endpoints of the major axis of an ellipse are (-4,-2) and (8,-2). The endpoints of the minor axis are (2,3) and (2,-7). Find the equation of this ellipse.

Plot those 4 points



Draw the major axis:



Notice that the major axis is 12 units long.
Therefore since the major axis is 2a units long,
2a = 12 and the semi-major axis, a = 6.

Draw the minor axis:



Notice that the minor axis is 10 units long.
Therefore since the minor axis is 2b units long,
2b = 10 and the semi-minor axis, b = 5.

Notice that the major and minor axis cross at the
point (2, -2).  So that is the center of the
ellipse, so (h,k) = (2,-2)

Sketch in the ellipse:

   

The equation of an ellipse whose major axis 
is horizontal is

 = 

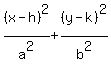We have observed fom the graph that a = 6,
b = 5, and (h, k) = (2,-2), so substituting, we have

 = 

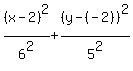or

 = 

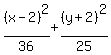Edwin