|
Question 1209099: Write the equation for the perpendicular bisector of the line segment connecting the points (-3,12) and (-5,12) in the form y = mx + b.
Note: The perpendicular bisector of the line segment \overline{AB} is the line
that passes through the midpoint of \overline{AB} and is perpendicular to \overline{AB}.
Answer by ikleyn(52817)   (Show Source):
You can put this solution on YOUR website! .
Write the equation for the perpendicular bisector of the line segment
connecting the points (-3,12) and (-5,12) in the form y = mx + b.
Note: The perpendicular bisector of the line segment \overline{AB} is the line
that passes through the midpoint of \overline{AB} and is perpendicular to \overline{AB}.
~~~~~~~~~~~~~~~~~~~~~~~~~~
You are lucky, since this problem is extremely simple.
Notice that y-coordinates of the two given points are the same number 12.
It means that the segment connecting the points is horizontal line y= 12.
Hence, the perpendicular line must be vertical x= const.
This constant value must be x-coordinate of the mid-point.
x-coordinate of the mid-point is the arithmetic mean of x-coordinates of endpoints.
Hence, const = 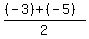 =  = -4.
Thus the desired equation for the perpendicular bisector is x = -4. ANSWER
Solved.
-------------------
Notice that it is IMPOSSIBLE to write an equation for the required line in the form y = mx+b.
This form is applicable for all sloped lines, but does not work for vertical lines.
For vertical lines, this special form x= const does work.
So, your problem is a TRAP, in some sense.
Your task is to recognize this trap, and my task is to teach you recognizing such traps.
|
|
|
| |
