|
Question 1209092: The difference of two positive numbers is 9. What is the minimum sum of their squares?
Absolute extrema/optimization
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let m and n be the mystery numbers where m > n.
Both are positive.
There's a 9 unit gap between them to indicate m-n = 9 which can be rearranged to m = n+9.
p = m^2+n^2 = summing their squares
The goal is to make p as small as possible.
To do so, we need to make n as small as possible.
If n = 0, then m = n+9 = 0+9 = 9 and m^2+n^2 = 0^2+9^2 = 81
But n = 0 isn't allowed since n > 0.
If n approaches 0 from above, then m^2+n^2 approaches 81 from above.
Therefore, m^2+n^2 doesn't have a minimum.
We have asymptotic behavior going on.
A similar situation is to think of the graph y = 1/x
As x gets bigger, y approaches 0 but never actually gets there.
--------------------------------------------------------------------------
Summary: There is no minimum sum of the squares.
The sum of squares gets closer to 81 from above, but never actually arrives at this sum itself.
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The difference of two positive numbers is 9. What is the minimum sum of their squares?
Absolute extrema/optimization
~~~~~~~~~~~~~~~~~~~~~
Let x be a greater of these two real numbers; y be a smaller of these two real numbers.
Then x - y = 9, or x = y+9.
They want you find the minimum of  , which is , which is
 = = 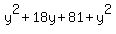 = = 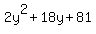 .
So, actually, we want to find the minimum of this quadratic function
f(y) = .
So, actually, we want to find the minimum of this quadratic function
f(y) = 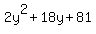 on the set of positive real numbers y > 0.
The global minimum of a quadratic function of the general form f(y) = ay^2 + by + c with positive
leading coefficient "a" is achieved at on the set of positive real numbers y > 0.
The global minimum of a quadratic function of the general form f(y) = ay^2 + by + c with positive
leading coefficient "a" is achieved at 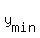 = =  . In this case . In this case
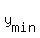 = = 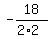 = -4.5,
which is negative value out of the scope of our consideration.
In the area y > 0, we have the ascending branch of the parabola on the right from its minimum in negative
number. Had we consider the scope of non-negative real numbers y >= 0, then the minimum of the parabola
f(y) = = -4.5,
which is negative value out of the scope of our consideration.
In the area y > 0, we have the ascending branch of the parabola on the right from its minimum in negative
number. Had we consider the scope of non-negative real numbers y >= 0, then the minimum of the parabola
f(y) = 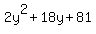 would be at y = 0 with the value f(0) = 81.
But, according to the problem, our scope is the set of positive numbers y > 0, and in this domain,
quadratic function f(y) = would be at y = 0 with the value f(0) = 81.
But, according to the problem, our scope is the set of positive numbers y > 0, and in this domain,
quadratic function f(y) = 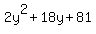 does not have the minimum, at all.
ANSWER. In the set of positive numbers, the function does not have the minimum, at all.
ANSWER. In the set of positive numbers, the function  with the restriction x-y = 9 has no minimum. with the restriction x-y = 9 has no minimum.
Solved.
---------------------
Above, I told you the whole story with all details.
I could explain everything in more short terms, simply noticing that
the parabola f(y) = 2y^2 + 18y + 81 has two positive terms 2y^2 and 18y
in the domain y > 0.
So, the values of f(y) go up as "y" goes to the right from zero,
which means that function f(y) raises there.
In opposite, function f(y) goes down as "y" approaches 0 from the right side.
But "y" never gets 0 in the positive domain - so we never get the minimum of f(y)
in the positive domain y > 0.
With these two explanations, you have now a complete picture and a complete vision to the problem.
|
|
|
| |