Question 1209088: There are two equilateral triangles with different areas, where O and O' are their circumcenters respectively. In the first, the distance OA is 9 cm, and in the second, the distance O'C' is 4√2 cm. Find the ratio of the area of the first to the area of the second.
https://ibb.co/Cz6tWsL
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
There are two equilateral triangles with different areas, where O and O' are t
heir circumcenters respectively. In the first, the distance OA is 9 cm,
and in the second, the distance O'C' is 4√2 cm.
Find the ratio of the area of the first to the area of the second.
https://ibb.co/Cz6tWsL
~~~~~~~~~~~~~~~~~~~~~~~~~
These equilateral triangles are similar (as any two equilateral triangles,
by three angles).
Their corresponding similar elements are OC and O'C'.
In the second triangle, we are given O'C' = 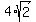 cm.
In the first triangle, we are given OA = 9 cm.
But triangle OAC is a right-angled 90°-60°-30°-triangle;
therefore, the hypotenuse OC is twice the leg OA,
so, the hypotenuse OC is 2*9 = 18 cm.
Thus, the ratio of corresponding linear dimensions in triangles is
OC 18 9 9*sqrt(2)
----- = ----------- = -------- = ----------.
O'C' 4*sqrt(2) 2*sqrt(2) 4
The ratio of the areas of the second triangle to the first triangle is the square
of the ratio of their corresponding linear elements, i.e. cm.
In the first triangle, we are given OA = 9 cm.
But triangle OAC is a right-angled 90°-60°-30°-triangle;
therefore, the hypotenuse OC is twice the leg OA,
so, the hypotenuse OC is 2*9 = 18 cm.
Thus, the ratio of corresponding linear dimensions in triangles is
OC 18 9 9*sqrt(2)
----- = ----------- = -------- = ----------.
O'C' 4*sqrt(2) 2*sqrt(2) 4
The ratio of the areas of the second triangle to the first triangle is the square
of the ratio of their corresponding linear elements, i.e.
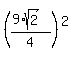 = = 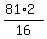 = = 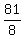 = 10.125. ANSWER = 10.125. ANSWER
Solved.
|
|
|