SOLUTION: In the diagram, AB = BC and BD=DC=CE. AB=4 cm. Find the length of AE, in cm. https://ibb.co/8KwNR4r

Algebra ->  Length-and-distance -> SOLUTION: In the diagram, AB = BC and BD=DC=CE. AB=4 cm. Find the length of AE, in cm. https://ibb.co/8KwNR4r      Log On


   

Question 1209058: In the diagram, AB = BC and BD=DC=CE. AB=4 cm. Find the length of AE, in cm.
https://ibb.co/8KwNR4r
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52814) About Me  (Show Source):
You can put this solution on YOUR website!
.
In the diagram, AB = BC and BD=DC=CE. AB=4 cm. Find the length of AE, in cm.
https://ibb.co/8KwNR4r
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

From the diagram, BC = AB = 4 cm.


Also from the diagram, BD = DC = BC/2 = 4/2 = 2 cm.


Hence, AE = DC = 2 cm.


From point E, draw a line parallel to BC till the intersection with AB at the point G.


Then GE is a perpendicular to AB and BG = CE = 2 cm.


Hence, AG = 4 - 2 = 2 cm.


Thus triangle AGE is a right angled triangle with the legs GE = 4 and AG = 2 cm.


Then the hypotenuse AE = sqrt%284%5E2+%2B+2%5E2%29 = sqrt%2820%29 = 2%2Asqrt%285%29 cm = 4.472 cm  (approximately).


ANSWER.  AE = 2%2Asqrt%285%29 = 4.472 cm  (approximately).

Solved.



Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Answer:
Exact length = 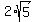2%2Asqrt%285%29 cm
Approximate length = 4.47214 cm
This approximate value will slightly vary depending how you round it.


Explanation

Let's place point B at the origin.
4 units above B is point A(0,4)

AB = BC = 4
Since BC = 4, we move 4 units to the right of B to arrive at C(4,0)

BD = DC tells us that D is the midpoint of BC, so BD = DC = CE = 2

From point C move 2 units up to arrive at E(4,2)

We can use the distance formula to find out how far it is from A(0,4) to E(4,2)
d+=+sqrt%28+%28x1-x2%29%5E2+%2B+%28y1-y2%29%5E2+%29

d+=+sqrt%28+%280-4%29%5E2+%2B+%284-2%29%5E2+%29 Plug in (x1,y1) = (0,4) and (x2,y2) = (4,2)

d+=+sqrt%28+%28-4%29%5E2+%2B+%282%29%5E2+%29

d+=+sqrt%28+16+%2B+4+%29

d+=+sqrt%28+20+%29

d+=+sqrt%284%2A5%29

d+=+sqrt%284%29%2Asqrt%285%29

d+=+2%2Asqrt%285%29

d+=+4.47214

Segment AE is exactly 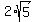2%2Asqrt%285%29 cm long. This approximates to 4.47214 cm.

--------------------------------------------------------------------------

A slight alternate route:

From point E, draw a horizontal line until reaching the y axis. This forms right triangle EGA where G is on the same level as E and directly below point A.


Let's get rid of any points or lines we don't need.


We have a right triangle with horizontal leg of GE = 4 and vertical leg GA = 2
Use the Pythagorean theorem a%5E2%2Bb%5E2=c%5E2 to determine 4%5E2%2B2%5E2+=+c%5E2 solves to c+=+sqrt%2820%29+=+2%2Asqrt%285%29+=+4.47214 which is the hypotenuse of this right triangle. And it's also the distance from A to E.

As you can probably tell (or know by now), the distance formula is a modified version of the Pythagorean theorem.