SOLUTION: ABC is an equilateral triangle. DE and DF are perpendiculars drawn from D to the sides shown. DE=4 cm and DF = 26 cm. Find the length, in cm, of the altitude AG. https://ibb.co/4j

Algebra ->  Length-and-distance -> SOLUTION: ABC is an equilateral triangle. DE and DF are perpendiculars drawn from D to the sides shown. DE=4 cm and DF = 26 cm. Find the length, in cm, of the altitude AG. https://ibb.co/4j      Log On


   

Question 1209057: ABC is an equilateral triangle. DE and DF are perpendiculars drawn from D to the sides shown. DE=4 cm and DF = 26 cm. Find the length, in cm, of the altitude AG.
https://ibb.co/4jLR8TF
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52835) About Me  (Show Source):
You can put this solution on YOUR website!
.
ABC is an equilateral triangle. DE and DF are perpendiculars drawn from D to the sides shown.
DE=4 cm and DF = 26 cm. Find the length, in cm, of the altitude AG.
https://ibb.co/4jLR8TF
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

Connect points D and G by a straight line.

This line divides triangle ABC in two triangles ABD and ACD.


So, the area of the whole triangle ABC is the sum of the areas of triangles ABD and ACD

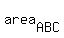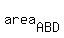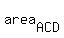    area%5BABC%5D = area%5BABD%5D + area%5BACD%5D.    (1)


Let "a" be the side length of the equilateral triangle ABC.


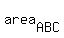Then the area of triangle ABC is  area%5BABC%5D = %281%2F2%29%2Aa%2AAG;

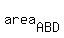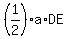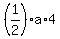     the area of triangle ABD is  area%5BABD%5D = %281%2F2%29%2Aa%2ADE = %281%2F2%29%2Aa%2A4;

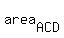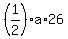     the area of triangle ACD is  area%5BACD%5D = %281%2F2%29%2Aa%2ADF = %281%2F2%29%2Aa%2A26.


So, we can write equation (1) in the form

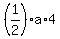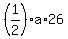    %281%2F2%29%2Aa%2AAG = %281%2F2%29%2Aa%2A4 + %281%2F2%29%2Aa%2A26.    (2)


In this equation, reduce the common factor  %281%2F2%29%2Aa  in both sides.  You will get then

    AG = 4 + 26 = 30.


At this point, the solution is complete, and you get this


ANSWER.  AG = 30 cm.

Solved.

----------------------

This problem is a classic,

and the solution,  which I provided in my post,  is a classic version,  too.

It provides a clear idea in clean form with the minimum calculations, and makes
the problem and the solution interesting, attractive, informative and educative.


This problem is one of the most brilliant among simple problems about triangles.
Such problems should be treated with reverence, and their classical solutions
should be passed on from generation to generation in that beautiful form as we
know them from our predecessors.



Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!
ABC is an equilateral triangle. DE and DF are perpendiculars drawn from D to the sides shown. DE=4 cm and DF = 26 cm. 
Find the length, in cm, of the altitude AG.
https://ibb.co/4jLR8TF

As ΔABC is equilateral, ∡B = ∡C = 60o

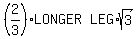
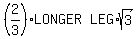
From right ΔBED, hypotenuse BD = %282%2F3%29+%2A+matrix%281%2C2%2C+LONGER%2C+LEG%29+%2A+sqrt%283%29
                              

From right ΔCFD, hypotenuse DC = %282%2F3%29+%2A+matrix%281%2C2%2C+LONGER%2C+LEG%29+%2A+sqrt%283%29
                              

So, one side of equilateral triangle ABC, BC = BD + DC = 

AC is also highlight%28highlight%2820sqrt%283%29%29%29

As an altitude from ANY vertex of ANY equilateral triangle, BISECTS that vertex' opposite side, altitude AG
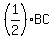BISECTS BC, and therefore, BG = GC = %281%2F2%29BC = 

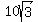Since AC = 20sqrt%283%29, and GC = 10sqrt%283%29, we use the PYTHAGOREAN THEOREM formula to get: 
                                                                                       30 cm = AG