Question 1209055: In the diagram, ABCD is a parallelogram with AB=37 cm. AD is a semi- circle.
The area of the parallelogram is 518 cm^2, and < ADC = 60°. Find the area of the shaded region in cm^2.
https://ibb.co/xs0HGmk
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In the diagram, ABCD is a parallelogram with AB=37 cm. AD is a semi- circle.
The area of the parallelogram is 518 cm^2, and < ADC = 60°.
Find the area of the shaded region in cm^2.
https://ibb.co/xs0HGmk
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Use the formula for the area of a parallelogram
area = 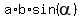 ,
where "a" and "b" are any two adjacent sides of the parallelogram and ,
where "a" and "b" are any two adjacent sides of the parallelogram and  is
the concluded angle between these sides.
In our case AB = 37, AD is unknown, is
the concluded angle between these sides.
In our case AB = 37, AD is unknown,  = 180°-60° = 120°. So, we have this equation
518 = 37*AD*sin(120°) = 37* = 180°-60° = 120°. So, we have this equation
518 = 37*AD*sin(120°) = 37*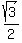 *AD,
hence
AD = *AD,
hence
AD =  = = 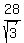 cm.
AD is the diameter, the shaded area is the semi-circle.
Hence, the area of the shaded area is cm.
AD is the diameter, the shaded area is the semi-circle.
Hence, the area of the shaded area is
 = = 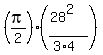 = =  = =  = =  = = 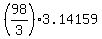 = 102.625 cm^2 (approximately).
ANSWER. The area of the shaded area is = 102.625 cm^2 (approximately).
ANSWER. The area of the shaded area is  cm^2, or about 102.625 cm^2. cm^2, or about 102.625 cm^2.
Solved.
|
|
|