Assuming that x \neq -5, simplify (2x + 10)^4 - (x + 5)^3 + \frac{4x^2 - 5x + 17}{(x + 5)^2}.
Write the expression as a single fraction.
I don't know that notation. It sure doesn't work on this site because it stays
just like you typed it. I asked AI, and it said it meant to simplify this:
 which would be written
(2x+10)^4-(x+6)^3 + (4x^2-5x+17)/(x+5)^2, x<>-5
in standard notation.
I doubt that that monster can be written much simpler than it already is:
First I'll divide out the third term, which is a fraction:
which would be written
(2x+10)^4-(x+6)^3 + (4x^2-5x+17)/(x+5)^2, x<>-5
in standard notation.
I doubt that that monster can be written much simpler than it already is:
First I'll divide out the third term, which is a fraction:
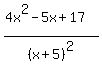

 4
x2 + 10x + 25)4x2 - 5x + 17
4x2 + 40x + 100
-45x - 83
4
x2 + 10x + 25)4x2 - 5x + 17
4x2 + 40x + 100
-45x - 83
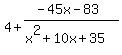

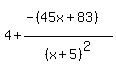

 Next we'll simplify the first two terms, using the binomial expansion:
Next we'll simplify the first two terms, using the binomial expansion:





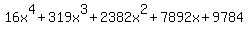 Now we'll add the simplification of the fraction term
Now we'll add the simplification of the fraction term
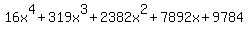


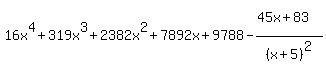 ,
,  Not a heck of a lot simpler.
Edwin
Not a heck of a lot simpler.
Edwin