Question 1208996: ABCD is a trapezoid in which AD: BC=3:5. If the area of
triangle AMD is 315 cm2, find the area of the trapezoid is, in cm2.
https://ibb.co/HTrxtP9
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 2240 square cm
Explanation

AD is parallel to BC due to the arrow markers.
These parallel segments allow us to determine these two facts:
angle ADB = angle DBC
angle DAC = angle BCA
The reason for each is the Alternate Interior Angle Theorem.
We can then use the Angle Angle Theorem to prove triangle AMD is similar to triangle CMB.
Segments AD and BC are in ratio 3:5
That scales up to 3x:5x
AD = 3x
BC = 5x
where x is some positive real number.
Rephrased another way: AD = (3/5)*BC = 0.6BC
Let h be the height of triangle CMB
(3/5)h = 0.6h is the height of triangle AMD because the triangles are similar.
area of triangle = 0.5*base*height
areaAMD = 0.5*AD*0.6h
areaAMD = 0.5*3x*0.6h
areaAMD = 0.9x*h
0.9x*h = 315
x*h = 315/0.9
x*h = 350
Let's call this equation (1) to use later.
Since h and 0.6h are the heights of triangles CMB and AMD respectively, this means the height of the trapezoid is h+0.6h = 1.6h
area of trapezoid = 0.5*height*(base1+base2)
areaABCD = 0.5*1.6h*(AD+BC)
areaABCD = 0.5*1.6h*(3x+5x)
areaABCD = 0.5*1.6h*(8x)
areaABCD = 0.5*1.6*8*(x*h)
areaABCD = 0.5*1.6*8*(350) ........ applying equation (1)
areaABCD = 2240 square cm
I used GeoGebra to confirm the answer is correct.
A similar question is found here
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
ABCD is a trapezoid in which AD: BC=3:5. If the area of
triangle AMD is 315 cm2, find the area of the trapezoid, in cm2.
https://ibb.co/HTrxtP9
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will give another solution, to get you totally different view on this problem.
 Triangles AMD and BMC are similar (since their three angles are congruent, in pairs).
The similarity coefficient is k = 5/3, from the greater triangle to the smaller.
Lat a = AM, b = BM, c = CM and D = DM.
Then b =
Triangles AMD and BMC are similar (since their three angles are congruent, in pairs).
The similarity coefficient is k = 5/3, from the greater triangle to the smaller.
Lat a = AM, b = BM, c = CM and D = DM.
Then b = 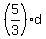 ; c = ; c = 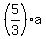 , due to similarity.
For any triangle with the side p and q and the concluded angle , due to similarity.
For any triangle with the side p and q and the concluded angle  ,
the area of this triangle is ,
the area of this triangle is  .
So, for the area of triangle AMD we have .
So, for the area of triangle AMD we have  = =  = 315 cm^2.
Here M is the angle between sides a = AM and d = DM .
Next, = 315 cm^2.
Here M is the angle between sides a = AM and d = DM .
Next,  = =  = = 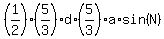 ,
where N is the supplementary angle to M.
Since sin(N) = sin(M), we can re-group the formula above and to get ,
where N is the supplementary angle to M.
Since sin(N) = sin(M), we can re-group the formula above and to get
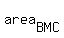 = = 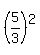 . . = = 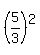 *area(AMD) = *area(AMD) = 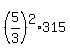 = =  = 25*35 = 875.
This calculation re-tells us a well known fact that the areas
of similar triangles do relate as the square of the similarity coefficient.
Now let's consider the most interesting things - the areas of triangles adjacent to lateral sides. = 25*35 = 875.
This calculation re-tells us a well known fact that the areas
of similar triangles do relate as the square of the similarity coefficient.
Now let's consider the most interesting things - the areas of triangles adjacent to lateral sides.
 = = 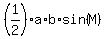 = = 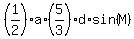 = =  = = 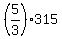 = 5*105 = 525, = 5*105 = 525,
 = =  = = 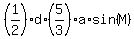 = =  = = 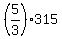 = 5*105 = 525.
Thus the total area of the trapezoid ABCD is 315 + 875 + 525 + 525 = 2240 cm^2. = 5*105 = 525.
Thus the total area of the trapezoid ABCD is 315 + 875 + 525 + 525 = 2240 cm^2.
At this point, the problem is solved completely.
The lesson to learn from this my solution:
if you are given a trapezoid, divided by its diagonals in four triangles, then
(a) the triangles, adjacent to the bases, always are similar;
(b) the triangles adjacent to lateral sides always have equal areas.
If, in addition, you are given the area "a" of a triangle adjacent to a base and the base-to-base ratio "k", then
(c) the areas of all triangles of the division can be easily found using the similarity coefficient:
- the area of the opposite triangle is 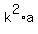 ; ;
- the areas of the triangles adjacent to lateral sides are k*a;
- the whole area of the trapezoid, in terms of " a " and " k " is 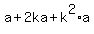 = =  . .
|
|
|