Question 1208989: A 20-pound bag of Economy brand cement mix contains 25% cement and 75% sand. How much pure cement must be added to produce a cement mix that is 40% cement?
I think the equation should look like this:
%•amount + %•amount = %(mixture)
0.25(20) + 0.75(x) = 0.40(x + 20)
Is this correct?
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52903)   (Show Source):
You can put this solution on YOUR website! .
A 20-pound bag of Economy brand cement mix contains 25% cement and 75% sand.
How much pure cement must be added to produce a cement mix that is 40% cement?
I think the equation should look like this:
%•amount + %•amount = %(mixture)
0.25(20) + 0.75(x) = 0.40(x + 20)
Is this correct?
~~~~~~~~~~~~~~~~~~~~~~~
This is wrong.
I will not explain, why it is wrong.
I will write a correct solution, instead.
Assume you add x pounds of pure cement.
Now the total mass is 20+x pounds; the portion of the pure cement is 0.25*20+x pounds.
You want
0.25*20 + x = 0.4*(20+x) pounds.
It is your setup equation to solve and to find x.
Now I solve it for you step by step. Watch my steps.
5 + x = 8 + 0.4x,
x - 0.4x = 8 - 5,
0.6x = 3,
x =  =  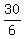= 5 pounds of the pure cement to add (rounded). ANSWER
Solved.
Answer by MathTherapy(10557)  (Show Source):
You can put this solution on YOUR website!
A 20-pound bag of Economy brand cement mix contains 25% cement and 75% sand. How much pure cement must be added to produce a cement mix that is 40% cement?
I think the equation should look like this:
%•amount + %•amount = %(mixture)
0.25(20) + 0.75(x) = 0.40(x + 20)
Is this correct?
No, it's NOT.
Initial amount of cement (C): .25(20)
Amount of cement (C) to be added: 100%, or 1(C)
Resulting CEMENT (C) in final mixture: .4(20 + C)
Cement + Cement = Cement
.25(20) + 1(C) = .4(20 + C) ===> .25(20) + C = .4(20 + C)
Now, solve for C, the amount of cement to be added.
|
|
|
