.
A motorboat maintained a constant speed of 15 miles per hour relative to the water
 is going 10 miles upstream and then returning.
is going 10 miles upstream and then returning.
The total time for the trip was 1.5 hours. Find the speed of the current.
~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x be the speed of the current, in miles per hour.
The motorboat' speed with the current is 15+x mph,
and against the current is 15-x mph.
Write and use the time equation
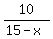 +
+ 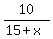 = 1.5 hours (1)
for the total trip.
To solve, multiply both sides by (15-x)*(15+x) = 225 - x^2. You will get
10(15+x) + 10*(15-x) = 1.5*(225-x^2),
300 = 1.5*225 - 1.5*x^2,
600 = 3*225 - 3x^2,
3x^2 = 675 - 600, 3x^2 = 75, x^2 = 75/3 = 25,
x =
= 1.5 hours (1)
for the total trip.
To solve, multiply both sides by (15-x)*(15+x) = 225 - x^2. You will get
10(15+x) + 10*(15-x) = 1.5*(225-x^2),
300 = 1.5*225 - 1.5*x^2,
600 = 3*225 - 3x^2,
3x^2 = 675 - 600, 3x^2 = 75, x^2 = 75/3 = 25,
x =  = 5 mph.
CHECK equation (1):
= 5 mph.
CHECK equation (1): 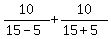 =
=  = 1
= 1 hours = 1.5 hours.
ANSWER. The current speed is 5 miles per hour.
hours = 1.5 hours.
ANSWER. The current speed is 5 miles per hour.
Solved.