Question 1208932: I would like to see the prove for these two questions.
1. If a > 0, show that the solution set of the inequality x^2 < a consists of all numbers x for which -sqrt{a} < x < sqrt{a}.
2. If a > 0, show that the solution set of the inequality x^2 > a consists of all numbers x for which x < -sqrt{a} or x > sqrt{a}.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1. If 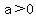 , show that the solution set of the inequality , show that the solution set of the inequality 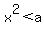 consists of all numbers x for which consists of all numbers x for which  .
Let us assume for contradiction that there exists x such that .
Let us assume for contradiction that there exists x such that
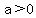 , yet , yet 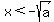 Since
Since 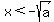 , x is negative for it is less than a negative number.
Then -x is a positive number and , x is negative for it is less than a negative number.
Then -x is a positive number and
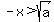 [both sides are positive]. Therefore, [both sides are positive]. Therefore,
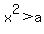 which contradicts which contradicts 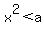 .
That's half the proof.
Now assume for contradiction that there exists x such that .
That's half the proof.
Now assume for contradiction that there exists x such that
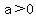 such that such that 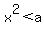 , yet , yet 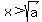 Since
Since 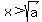 , , 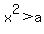 which contradicts which contradicts 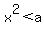 Thus the proof is done, and
Thus the proof is done, and
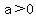 , , 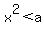 implies implies  .
------------------
2. If .
------------------
2. If 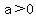 , show that the solution set of the inequality , show that the solution set of the inequality 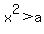 consists of all numbers x for which
consists of all numbers x for which 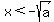 or or 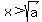 .
Assume for contradiction that there exists x such that .
Assume for contradiction that there exists x such that
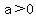 and and 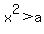 , yet , yet 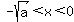 Then both
Then both 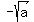 and x are negative numbers, and thus -x is a
positive number. and x are negative numbers, and thus -x is a
positive number.
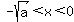 implies implies 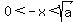 thus thus 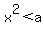 which contradicts
which contradicts  That's half the proof.
Next, assume for contradiction that there exists x such that
That's half the proof.
Next, assume for contradiction that there exists x such that
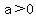 and and 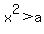 , yet , yet  Then
Then  implies implies 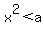 which contradicts which contradicts  .
Then .
Then 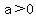 , , 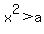 implies implies 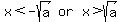 Edwin
Edwin
|
|
|