Question 1208918: A history class is comprised of 5
female and
9 male students. If the instructor of the class randomly chooses
8 students from the class for an oral exam, what is the probability that
3 female students and
5 male students will be selected? Round your answer to
decimal places
Found 4 solutions by mccravyedwin, math_tutor2020, ikleyn, Edwin McCravy:
Answer by mccravyedwin(408)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 0.41958 approximately
The exact value as a fraction is 60/143.
Explanation
Let's see how many ways there are to select the girls.
The teacher has 5 choices for the 1st slot, then 4 for the next, and 3 for the last.
5*4*3 = 60 permutations of girls if order mattered.
I'll assume that order doesn't matter, so we divide by 3! = 3*2*1 = 6 because this is the number of ways to arrange any trio of people. - ABC
- ACB
- BAC
- BCA
- CAB
- CBA
Therefore the teacher has 60/6 = 10 different ways to pick the girls sub-group where order doesn't matter.
Another way to get to this result (10) is to use the nCr combination formula with n = 5 and r = 3.
That formula is
n C r = (n!)/(r!(n-r)!)
There are many calculators that will quickly calculate nCr values.
You can use this combinatorics calculator
https://www.mathsisfun.com/combinatorics/combinations-permutations-calculator.html
to not only calculate the nCr value but also list out the possible combos.
Refer to the "list them" section.
Another way to compute the nCr value is to use Pascal's Triangle.
Use any method you prefer to find that:
There are 9C5 = 126 ways to select the boys.
There are 14C8 = 3003 ways to pick the group of eight people regardless of gender.
Side note:
Notation like 14C8 is equivalent to writing C(14,8)
------------------------------
So we found there are 10 ways to pick the girls and 126 ways to pick the boys.
What do we do with these numbers?
Imagine we had a table that is 10 columns across and 126 rows tall.
Of course such a massive table is a thought exercise only and not something to actually draw out on paper.
This table has 10*126 = 1260 inner cells.
Each inner cell represents a different combo of 3 girls and 5 boys.
It might help to make a much smaller scaled down version of this table so you can see what I'm talking about.
Anyways the punchline of that previous paragraph is that we have 1260 different combos of three girls + five guys out of 3003 different possibilities.
1260/3003 = 60/143 = 0.41958 approximately.
This is somewhat close to 42%
Your instructions mention "Round your answer to ____ decimal places" but the value in the blank is missing. It appears to be a strange error of some kind.
Answer by ikleyn(52809)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A history class is comprised of 5 female and 9 male students.
If the instructor of the class randomly chooses 8 students from the class for an oral exam,
what is the probability that 3 female students and 5 male students will be selected?
Round your answer to decimal places.
~~~~~~~~~~~~~~~~~~~~~~~
The correct formula for the probability is
P = 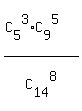 Here the denominator is the number of all possible different unordered sets of 8 students
to be selected from 5+9 = 14 students.
In the numerator, C[5]^3 represents the number of all possible different triplets of female
students selected from 5 female students;
C[9]^5 represents the number of all possible different quintuplets of male
students selected from 9 male students.
Now,
Here the denominator is the number of all possible different unordered sets of 8 students
to be selected from 5+9 = 14 students.
In the numerator, C[5]^3 represents the number of all possible different triplets of female
students selected from 5 female students;
C[9]^5 represents the number of all possible different quintuplets of male
students selected from 9 male students.
Now, 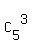 = = 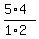 = 10; = 10;
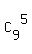 = = 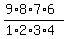 = 126; = 126;
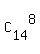 = = 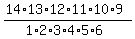 = 3003.
Therefore, the ANSWER is
P = = 3003.
Therefore, the ANSWER is
P = 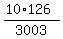 = 0.41958042
and you can round it in any way you need. = 0.41958042
and you can round it in any way you need.
Solved.
The calculations of the binomial coefficients can be done manually or using technology.
I personally use MS Excel in my computer, by copying-pasting the formula into it,
or the standard Excel function COMBIN.
Here in my solution, I used the notion/(the conception) of COMBINATIONS.
Actually, when you get such a problem, it is assumed in the regular/normal course of education
that you are familiar with this conception and relevant formulas.
If you are not familiar with it, in clear and compact form it is given in the lessons
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
in this site.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
|
|
|