.
Solve for x.
2sinx + 2tanx = 0
~~~~~~~~~~~~~~~~~~~~~~~
You want to solve
2sin(x) + 2tan(x) = 0.
The domain of this equation are all real numbers except of x = 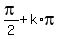 , where cos(x) = 0.
Rewrite in the form
2sin(x) +
, where cos(x) = 0.
Rewrite in the form
2sin(x) +  = 0.
In the domain, multiply both sides by
= 0.
In the domain, multiply both sides by  .
Since cos(x) =/= 0, you will get an equivalent equation
sin(x)*cos(x) + sin(x) = 0.
Factor
sin(x)*(cos(x) + 1) = 0.
So, either sin(x) = 0, giving the solutions x =
.
Since cos(x) =/= 0, you will get an equivalent equation
sin(x)*cos(x) + sin(x) = 0.
Factor
sin(x)*(cos(x) + 1) = 0.
So, either sin(x) = 0, giving the solutions x =  , k = 0, +/-1, +/-2, . . . (1)
or cos(x) + 1 = 0, cos(x) = -1, giving x =
, k = 0, +/-1, +/-2, . . . (1)
or cos(x) + 1 = 0, cos(x) = -1, giving x = 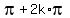 , k = 0, +/-1, +/-2, . . . (2)
The set (2) is part of set (1) - so, the general solution to the given equation is the set
x =
, k = 0, +/-1, +/-2, . . . (2)
The set (2) is part of set (1) - so, the general solution to the given equation is the set
x =  , k = 0, +/-1, +/-2, . . .
ANSWER. The general solution to the given equation is the set x =
, k = 0, +/-1, +/-2, . . .
ANSWER. The general solution to the given equation is the set x =  , k = 0, +/-1, +/-2, . . .
, k = 0, +/-1, +/-2, . . .
Solved.