Question 1208880: If (a + 1)(b + 1)(a + b) = 1530
and a³ + b³ = 1241
then a + b = ?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52799)   (Show Source):
You can put this solution on YOUR website! .
If (a + 1)(b + 1)(a + b) = 1530
and a^3 + b^3 = 1241
then a + b = ?
~~~~~~~~~~~~~~~~~~~~~
It admits (= it has) fantastically brilliant solution.
First, (1 + a)(1 + b)(a + b) = (1 + a + b + ab)*(a+b) = (a+b) + (a+b)^2 + ab*(a+b).
Next, a^3 + b^3 = (a+b)*(a^2 - ab + b^2) = (a+b)*((a+b)^2-3ab) = (a+b)^3 - 3ab*(a+b).
Thus you have these two equations
(a+b) + (a+b)^2 + ab*(a+b) = 1530 (1)
(a+b)^3 - 3ab*(a+b) = 1241 (2)
Multiply equation (1) by 3; keep equation (2) as is. Then add them. You will get
3(a+b) + 3(a+b)^2 + (a+b)^3 = 3*1530 + 1241,
or
3(a+b) + 3(a+b)^2 + (a+b)^3 = 5831.
Add 1 to both sides
1 + 3(a+b) + 3(a+b)^2 + (a+b)^3 = 5832.
Notice that the left side is ((a+b)+1)^3.
So, the last equation is
((a+b)+1)^3 = 5832.
Take cube root of both sides
(a+b)+1 = 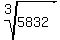 = 18.
From this, get
a+b = 18-1 = 17.
ANSWER. If (1 + a)(1 + b)(a + b) = 1530 and a^3 + b^3 = 1241, then a+b = 17.
Solved.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
The other tutor has a great solution.
Perhaps it's the most efficient pathway to solve.
I'll provide another method.
w = a+b
(a+1)(b+1)(a+b) = 1530
(ab+a+b+1)(a+b) = 1530
(ab+w+1)w = 1530
ab+w+1 = 1530/w
ab = 1530/w - w - 1
Let's call this equation (1) to use later.
Then notice how,
w = a+b
w^2 = (a+b)^2
w^2 = a^2+2ab+b^2
w^2-3ab = a^2+2ab+b^2-3ab
w^2-3ab = a^2-ab+b^2
Let's call this equation (2)
Use the sum of cubes formula to say the following
a^3+b^3 = (a+b)(a^2-ab+b^2)
a^3+b^3 = w(w^2-3ab) ............................. plug in equation (2)
1241 = w(w^2-3*( 1530/w - w - 1 )) ............... plug in equation (1)
1241 = w^3-3w*( 1530/w) + 3w^2 + 3w
1241 = w^3-4590 + 3w^2 + 3w
w^3-4590 + 3w^2 + 3w-1241 = 0
w^3 + 3w^2 + 3w - 5831 = 0
From here you can use a graphing calculator to graph y = x^3 + 3x^2 + 3x - 5831
The only real number root is x = 17. This is where the cubic curve crosses the x axis. You'll likely need to adjust your window to be able to see this root.
As a check,
x^3 + 3x^2 + 3x - 5831 = 0
(17)^3 + 3(17)^2 + 3(17) - 5831 = 0
4913 + 867 + 51 - 5831 = 0
0 = 0
This proves that w = 17 is a solution to w^3 + 3w^2 + 3w - 5831 = 0
Through trial and error (aided with a spreadsheet), you can determine that a = 8 and b = 9 satisfy the two given equations.
| (a+1)*(b+1)*(a+b) = 1530(8+1)*(9+1)*(8+9) = 15309*10*17 = 15301530 = 1530 .... works | a^3+b^3 = 12418^3+9^3 = 1241512+729 = 12411241 = 1241 .... works |
So we conclude that a+b = 8+9 = 17
Due to symmetry, we could also say that a = 9 and b = 8.
Answer: 17
|
|
|
