Find the real solutions of the equations.
(A) 2x^(-2) - 3x^(-1) - 4 = 0
(B) [y/(y - 1)]^2 = 6[y/(y - 1)] + 7
~~~~~~~~~~~~~~~~~~~~~~~
I will solve equation (B).
(B) [y/(y - 1)]^2 = 6[y/(y - 1)] + 7.
Introduce new variable
t = 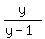 .
Then equation (1) takes the form
t^2 = 6t + 7.
Write it in the standard form quadratic equation
t^2 - 6t - 7 = 0.
Factor left side
(t-7)*(t+1) = 0.
The roots are t= 7 and t= -1.
Consider two cases.
1) t= 7. It means
.
Then equation (1) takes the form
t^2 = 6t + 7.
Write it in the standard form quadratic equation
t^2 - 6t - 7 = 0.
Factor left side
(t-7)*(t+1) = 0.
The roots are t= 7 and t= -1.
Consider two cases.
1) t= 7. It means 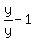 = 7, y = 7*(y-1), y = 7y - 7, 7 = 7y - y, 7 = 6y, y = 7/6.
2) t= -1. It means
= 7, y = 7*(y-1), y = 7y - 7, 7 = 7y - y, 7 = 6y, y = 7/6.
2) t= -1. It means 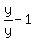 = -1, y = (-1)*(y-1), y = -y + 1, y + y = 1, 2y = 1, y = 1/2.
ANSWER. Equation (B) has two solutions: y= 1/2 and y= 7/6.
= -1, y = (-1)*(y-1), y = -y + 1, y + y = 1, 2y = 1, y = 1/2.
ANSWER. Equation (B) has two solutions: y= 1/2 and y= 7/6.
(B) is solved.