I won't do this for you, but I'll tell you what I would do.
I would use these two definite integrals:
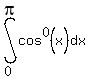

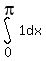




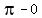













 together with this recursion formula from a table of integrals:
together with this recursion formula from a table of integrals:
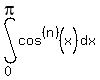


 Then find
Then find
 ,
, 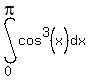 ,
, 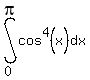 , etc.,
and see if you can find a pattern to the sequence of integrals, and then what
the integrals are approaching as n approaches infinity,
, etc.,
and see if you can find a pattern to the sequence of integrals, and then what
the integrals are approaching as n approaches infinity,
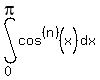 Edwin
Edwin