Question 1208824: A triangle has a perimeter of 96 m. and an area of 138 sq.m. What is the radius of the circle that maybe inscribed in this triangle.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 2.875 meters
This decimal value is exact and hasn't been rounded.
Explanation
For visual learners it often helps to draw a diagram if you're not sure where to start.
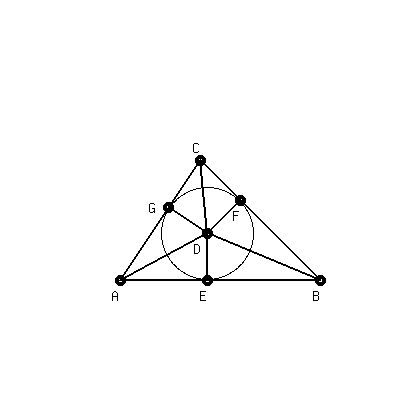
We have triangle ABC with a circle inscribed inside it. This circle is known as an incircle.
This is the largest possible circle to fit inside the triangle where none of the circle spills outside it. Think of it like a balloon inflating to fill up a triangular enclosure.
The center of the incircle, known as the incenter, is point D.
Points E,F,G are tangent to the circle and reside on sides AB, BC, AC in that order.
Segments DE, DF, DG are radii of the incircle (these radius lengths are known as the inradius).
Since they are radii of the same circle, we know that DE = DF = DG which will be used later on below.
Since point E is one of the tangent points, it means inradius DE is perpendicular to segment AB.
Similarly, DF is perpendicular to BC, and DG is perpendicular to CA.
Triangle ABC can be split into these three triangles
ABD, BCD, CAD
The base of triangle ABD is side AB.
The height of triangle ABD is the inradius segment DE.
Recall that the base and height are always perpendicular to each other.
area(triangle ABD) = 0.5*base*height = 0.5*AB*DE
Similarly,
area(BCD) = 0.5*BC*DF
area(CAD) = 0.5*CA*DG
which leads to,
area(ABC) = area(ABD)+area(BCD)+area(CAD)
area(ABC) = 0.5*AB*DE + 0.5*BC*DF + 0.5*CA*DG
area(ABC) = 0.5*AB*DE + 0.5*BC*DF + 0.5*CA*DG
area(ABC) = 0.5*AB*DE + 0.5*BC*DE + 0.5*CA*DE ............ substitute DE in for the other radii
area(ABC) = 0.5*DE*(AB+BC+CA)
area(ABC) = 0.5*inRadius*(perimeter of triangle ABC)
We have a nice formula that connects the area, perimeter, and inradius of a triangle.
Some textbooks will use this formula
triangleArea = inRadius*semiPerimeter
which is just a slight variation of the previous formula. The semi perimeter is half the perimeter.
i.e. semiperimeter = 0.5*perimeter
Let's solve for the inradius
area(ABC) = 0.5*inRadius*(perimeter of triangle ABC)
2*area(ABC) = inRadius*(perimeter of triangle ABC)
inRadius = 2*area(ABC)/(perimeter of triangle ABC)
Now use the info your teacher gave you.
inRadius = 2*area(ABC)/(perimeter of triangle ABC)
inRadius = 2*138/(96)
inRadius = 2.875 meters exactly.
|
|
|