Question 1208813: Solve for x.
(sin x + cos x)/(1 - tan x) = 0
Found 2 solutions by AnlytcPhil, ikleyn:
Answer by AnlytcPhil(1810)   (Show Source): (Show Source):
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve for x: (sin x + cos x)/(1 - tan x) = 0
~~~~~~~~~~~~~~~~~~~~
The solution in the post by Edwin is incomplete.
I came to bring a complete solution.
The domain (the set of real numbers, where left side of the equation
is defined) is tan(x) =/= 1.
So, the prohibited values of x are 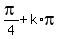 , k = 0, _/-1, +/-2, . . .
We are looking for solutions of the given equation that are in its domain.
In the domain, the given equation is equivalent to
sin(x) + cos(x) = 0, (1)
or
sin(x) = -cos(x). (2)
The solutions to this equation can not be with cos(x) = 0 (since then sin(x) = 1,
and this equation is not held) .
Therefore, we can divide both sides of equation (2) by cos(x). We get then
tan(x) = -1.
The solutions to this equation are
x = , k = 0, _/-1, +/-2, . . .
We are looking for solutions of the given equation that are in its domain.
In the domain, the given equation is equivalent to
sin(x) + cos(x) = 0, (1)
or
sin(x) = -cos(x). (2)
The solutions to this equation can not be with cos(x) = 0 (since then sin(x) = 1,
and this equation is not held) .
Therefore, we can divide both sides of equation (2) by cos(x). We get then
tan(x) = -1.
The solutions to this equation are
x = 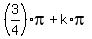 , or 135° + 180°*k, k = 0, +/-1, +/-2, . . .
ANSWER. The solutions to the given equation are x = , or 135° + 180°*k, k = 0, +/-1, +/-2, . . .
ANSWER. The solutions to the given equation are x = 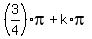 , or 135° + 180°*k, k = 0, +/-1, +/-2, . . . , or 135° + 180°*k, k = 0, +/-1, +/-2, . . .
Solved.
|
|
|