Question 1208810: The sum of 128 consecutive odd, positive integers is the greatest power of two less than 200 000. The sum of the least and the greatest of these integers is 2. Find N.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Something is obviously wrong with the problem as stated. If you have any 128 consecutive odd positive integers, the sum of the least and greatest of them can't be 2....
Fix the statement of the problem and re-post.
----------------------------------------------------------
UPDATE....
In my original response, I didn't get past the sum of the smallest and largest being equal to 2; I didn't even see the part of the problem that said "find N".
After seeing the response from tutor @ikleyn about N not being defined in the statement of the problem, it became clear to me what the statement of the problem was supposed to be:
The sum of 128 consecutive odd, positive integers is the greatest power of two less than 200 000. The sum of the least and the greatest of these integers is 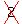 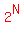 . Find N. . Find N.
This makes for a nice (and, as it turns out, a relatively easy) problem....
The largest power of 2 less than 200,000 is 2^17 = 131072
This is the sum of an arithmetic sequence of 128 consecutive odd integers. The sum of 128 terms of an arithmetic sequence is the sum of 64 pairs of numbers, each pair of which is equal to the sum of the least and greatest of the numbers in the sequence. But that sum is what the problem asks us to find. So the rest is easy:
64x = 131072
x = 131072/64 = 2048
ANSWER: 2048
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The sum of 128 consecutive odd, positive integers is the greatest power of two less than 200 000.
The sum of the least and the greatest of these integers is 2. Find N.
~~~~~~~~~~~~~~~~~~~~~~~~~~
Who is N to find it ?
|
|
|