Question 1208808: A tub can be filled with hot water in 18 minutes, or with cold water in 12 minutes. The tub can also be emptied when the plug is pulled out, in 9 minutes. Farley ran the hot water in his tub for 8 minutes, then both the cold and hot water together for 2 minutes, and then with the two taps still running, he accidentally pulled the plug. How long did it take, in minutes, for the tub to fill after the plug was pulled?
Found 5 solutions by greenestamps, josgarithmetic, ikleyn, math_tutor2020, MathTherapy:
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The fraction of the tub filled in 1 minute by the hot water tap alone is 1/18.
The fraction of the tub filled in 1 minute by both taps together is 1/18 + 1/12 = 2/36 + 3/36 = 5/36.
The fraction of the tub drained by the drain in 1 minute is 1/9.
When both taps and the drain are all open, the fraction of the tub filled in 1 minute is 5/36 - 1/9 = 5/36 - 4/36 = 1/36.
The hot water tap is run for 8 minutes. The fraction of the tub filled is 8(1/18) = 8/18 = 4/9.
Both taps are run for 2 minutes. The fraction of the tub filled in those 2 minutes is 2(5/36) = 10/36 = 5/18. The fraction of the tub now filled is 4/9 + 5/18 = 8/18 + 5/18 = 13/18; the fraction of the tub remaining to be filled is 5/18.
The fraction of the tub remaining to be filled is 5/18; the rate at which the tub is being filled with both taps and the drain all open is 1/36. The number of minutes needed to finish filling the tank after the drain is opened is (5/18)/(1/36) = (10/36)/(1/36) = 10.
ANSWER: 10 minutes
CHECK:
The hot water tap will have been running for 8+2+10 = 20 minutes; the cold water tap for 2+10 = 12 minutes; and the drain will have been open for 10 minutes. The tub should be full at the end of that time -- i.e, the fraction of the tub that should be full is 1.
20(1/18) + 12(1/12) - 10(1/9) = 20/18 + 1 - 10/9 = 1
Answer by josgarithmetic(39625)   (Show Source): (Show Source):
Answer by ikleyn(52857)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A tub can be filled with hot water in 18 minutes, or with cold water in 12 minutes.
The tub can also be emptied when the plug is pulled out, in 9 minutes.
Farley ran the hot water in his tub for 8 minutes,
then both the cold and hot water together for 2 minutes,
and then with the two taps still running, he accidentally pulled the plug.
How long did it take, in minutes, for the tub to fill after the plug was pulled?
~~~~~~~~~~~~~~~~~~~~~~~
The rate of filling the tub with the hot water is  of the tube volume per minute.
The rate of filling the tub with the cold water is of the tube volume per minute.
The rate of filling the tub with the cold water is  of the tube volume per minute.
The rate of draining the tub is of the tube volume per minute.
The rate of draining the tub is  of the tube volume per minute.
The rate of filling the tube in the first 8 minutes was of the tube volume per minute.
The rate of filling the tube in the first 8 minutes was  of the tube volume per minute.
The rate of filling the tube in the next 2 minutes was of the tube volume per minute.
The rate of filling the tube in the next 2 minutes was 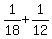 = = 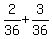 = = 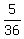 of the tube volume per minute.
The net rate of filling the tube in the last t minutes was of the tube volume per minute.
The net rate of filling the tube in the last t minutes was  = = 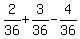 = =  of the tube volume per minute.
An equation to fill the tube under given conditions is of the tube volume per minute.
An equation to fill the tube under given conditions is
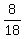 + + 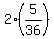 + + 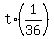 = 1.
Simplify and find t = 1.
Simplify and find t
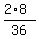 + + 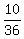 + + 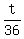 = 1, = 1,
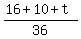 = 1,
26 + t = 36,
t = 36 - 26
t = 10.
ANSWER. It took 10 minutes to fill the tub after the plug was pulled. = 1,
26 + t = 36,
t = 36 - 26
t = 10.
ANSWER. It took 10 minutes to fill the tub after the plug was pulled.
Solved.
-------------------
To see many other similar (and different) problems on joint work,
solved with complete explanations to teach you, look into the lessons
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Selected joint-work word problems from the archive
Read them and get be trained in solving joint-work problems.
Consider these lessons as your textbook, handbook, guidebook, tutorials and (free of charge) home teacher,
which is always with you to help and to inspire.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 10 minutes
Explanation
Let's say the tub's capacity is 360 gallons.
I'm picking this value since 36 is the LCM of {18,12,9} and I tacked a zero at the end to make the volume seem more realistic.
The 360 can be changed to any value you want to get the same result at the end.
Discussion to find the LCM will be left out to keep this solution relatively short.
If the tub starts completely empty with the plug in place, and takes 18 minutes to fill up from the hot water tap, then the hot water faucet's fill rate is 360/18 = 20 gallons per minute.
rate = amountDone/time
The cold water tap needs 12 minutes when working alone, so the cold faucet fill rate is 360/12 = 30 gallons per minute.
Like with the previous paragraph, I'm assuming the tub starts off completely empty and the plug is in place.
In contrast, if the tub starts off completely full and the drain needs 9 minutes to empty fully, then the drain rate is 360/9 = 40 gallons per minute.
For this paragraph we assume the hot and cold water faucets are shut off.
----------------------------
"Farley ran the hot water in his tub for 8 minutes."
rate*time = amountDone
(20 gallons per min)*(8 min) = 160 gallons of hot water
"then both the cold and hot water together for 2 minutes"
rate*time = amountDone
(hotWaterFillRate + coldWaterFillRate)*(time) = amountDone
(20 gal per min + 30 gal per min)*(2 min) = amountDone
(50 gal per min)*(2 min) = 100 gallons of hot and cold water mixed
Farley will have 160+100 = 260 gallons of water at the 8+2=10 minute marker.
He needs another 360-260 = 100 gallons to fill up the tub.
At this point he accidentally pulled the plug.
The net rate is now 50-40 = 10 gallons per minute.
The positive result means the faucets win out and the tub fills up (albeit more slowly of course).
rate*time = amountNeededToGetDone
time = amountNeededToGetDone/rate
time = (100 gallons needed)/(10 gal per min)
time = 10 minutes
This is the duration of time after the plug is pulled to when the tub is completely full.
This does not account for the previous 10 minutes mentioned (meaning the total duration is 10+10 = 20 min)
In other words, 8 min hot water + 2 min hot&cold water + 10 min hot & cold & drain = 20 min total
A similar problem can be found here
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1204617.html
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A tub can be filled with hot water in 18 minutes, or with cold water in 12 minutes. The tub can also be emptied when the plug is pulled out, in 9 minutes. Farley ran the hot water in his tub for 8 minutes, then both the cold and hot water together for 2 minutes, and then with the two taps still running, he accidentally pulled the plug. How long did it take, in minutes, for the tub to fill after the plug was pulled?
Time tub can be filled with hot water: 18 minutes, which means that  of tub can be filled with hot water in 1 minute
Time tub can be filled with cold water: 12 minutes, which means that of tub can be filled with hot water in 1 minute
Time tub can be filled with cold water: 12 minutes, which means that  of tub can be filled with cold water in 1 minute
With hot water being run for 8 minutes, and both hot and cold water for 2 minutes, fraction of tub thatw's filled with hot
and cold water in those 10 minutes = of tub can be filled with cold water in 1 minute
With hot water being run for 8 minutes, and both hot and cold water for 2 minutes, fraction of tub thatw's filled with hot
and cold water in those 10 minutes = 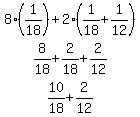

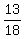 of tub was filled in the 8 minutes that the hot water ran for, alone, and the 2 minutes thereafter that both hot and cold ran, together
Therefore, of tub was filled in the 8 minutes that the hot water ran for, alone, and the 2 minutes thereafter that both hot and cold ran, together
Therefore,  of tub was left to be filled
Time tub can be emptied after plug is pulled: 9 minutes, which means that of tub was left to be filled
Time tub can be emptied after plug is pulled: 9 minutes, which means that  of tub can be EMPTIED in 1 minute
Now, with the plug being pulled, and fill-time being T, we get: of tub can be EMPTIED in 1 minute
Now, with the plug being pulled, and fill-time being T, we get:  Cross-multiplying, we get the TIME taken to fill the tub, after the plug was pulled, or T = 10 minutes.
Cross-multiplying, we get the TIME taken to fill the tub, after the plug was pulled, or T = 10 minutes.
|
|
|