|
Question 1208784: Adam, Ben and Calvin had a total of 540 marbles. Adam gave 1/4 of his marbles to Ben. Then, Ben gave 1/3 of his total number of marbles to Calvin. In the end, all the boys had the same number of marbles.
(a) How many marbles did each boy have in the end?
(b) How many marbles did Ben have at first?
Found 4 solutions by josgarithmetic, ikleyn, MathTherapy, greenestamps:
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
Answer by ikleyn(52791)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Adam, Ben and Calvin had a total of 540 marbles.
Adam gave 1/4 of his marbles to Ben. (1st exchange)
Then, Ben gave 1/3 of his total number of marbles to Calvin. (2nd exchange)
In the end, all the boys had the same number of marbles.
(a) How many marbles did each boy have in the end?
(b) How many marbles did Ben have at first?
~~~~~~~~~~~~~~~~~~~
Solution
(a) Part (a) is easy.
Indeed, at the beginning, the total number of marbles was 540.
In process of exchanges, the total number of marbles remains the same:
it did not change.
Therefore, since at the end all the boys had the same number of marbles,
this final number of marbles, which every boy had at the end was 540/3 = 180.
It is the ANSWER to question (a).
(b) At the last exchange, Ben gave 1/3 of his marbles to Calvin.
So, we can write this equations, describing this exchange
b - 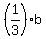 = 180, (1)
c + = 180, (1)
c + 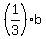 = 180, (2)
where "b" and "c" are the numbers of marbles that Ben and Calvin had before 2nd exchange.
From equation (1), = 180, (2)
where "b" and "c" are the numbers of marbles that Ben and Calvin had before 2nd exchange.
From equation (1), 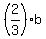 = 180, hence b = = 180, hence b = 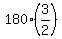 = 270.
Then equation (2) becomes
c + = 270.
Then equation (2) becomes
c + 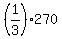 = 180,
or
c + 90 = 180,
giving c = 180 - 90 = 90.
So, before 2nd exchange and after 1st exchange Ben had 270 marbles; Calvin had 90 marbles.
Now for/from the 1st exchange, we have this equation = 180,
or
c + 90 = 180,
giving c = 180 - 90 = 90.
So, before 2nd exchange and after 1st exchange Ben had 270 marbles; Calvin had 90 marbles.
Now for/from the 1st exchange, we have this equation
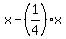 = 180, (3) = 180, (3)
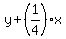 = 270. (4)
where "x" and "y" are the numbers of marbles that Adam and Ben had before 1st exchange
(i.e. originally).
From equation (3), we have = 270. (4)
where "x" and "y" are the numbers of marbles that Adam and Ben had before 1st exchange
(i.e. originally).
From equation (3), we have
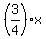 = 180, x = = 180, x = 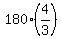 = 60*4 = 240.
From equation (4), we have = 60*4 = 240.
From equation (4), we have
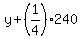 = 270,
y + 60 = 270,
y = 270 - 60 = 210.
At this point, the solution is complete.
ANSWER. Initially, Adam had 240 marbles; Ben had 210 marbles; Calvin had 90 marbles.
CHECK. 1st exchange: {240,210,90) ---> (180,270,90).
2nd exchange: (180,270,90) ---> (180,180,180). ! correct ! = 270,
y + 60 = 270,
y = 270 - 60 = 210.
At this point, the solution is complete.
ANSWER. Initially, Adam had 240 marbles; Ben had 210 marbles; Calvin had 90 marbles.
CHECK. 1st exchange: {240,210,90) ---> (180,270,90).
2nd exchange: (180,270,90) ---> (180,180,180). ! correct !
Solved.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Adam, Ben and Calvin had a total of 540 marbles. Adam gave 1/4 of his marbles to Ben. Then, Ben gave 1/3 of his total number of marbles to Calvin. In the end, all the boys had the same number of marbles.
(a) How many marbles did each boy have in the end?
(b) How many marbles did Ben have at first?
The number of marbles REMAINED the SAME throughout all the back-and-forth exchanges.
Since the total number they began with was 540, and since ALL 3 ended up with the same number,
each ended up with 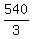 = 180 marbles.
Now, let amount Adam and Ben started with, be A and B, respectively
After Adam gave = 180 marbles.
Now, let amount Adam and Ben started with, be A and B, respectively
After Adam gave  of his marbles to Ben, Adam then had of his marbles to Ben, Adam then had  remaining
Since Adam had 180 remaining after his exchange with Ben, we get: remaining
Since Adam had 180 remaining after his exchange with Ben, we get:  Amount Adam started with, or
Amount Adam started with, or  After receiving
After receiving  of Adam's marbles, or of Adam's marbles, or  , Ben then had , Ben then had 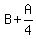 . But, after giving . But, after giving  of his
REMAINING marbles to Calvin, Ben then had of his
REMAINING marbles to Calvin, Ben then had  remaining
As Ben had 180 remaining after his exchanges with Adam and Calvin, we get: remaining
As Ben had 180 remaining after his exchanges with Adam and Calvin, we get: 
 -- Substituting 240 for A -- Substituting 240 for A
 Amount Ben started with, or
Amount Ben started with, or 
Answer by greenestamps(13200)   (Show Source): (Show Source):
|
|
|
| |