SOLUTION: Find the range of y = x/(x - 5).

Algebra ->  Rational-functions -> SOLUTION: Find the range of y = x/(x - 5).       Log On


   

Question 1208753: Find the range of y = x/(x - 5).

Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13215) About Me  (Show Source):
You can put this solution on YOUR website!


To find the range of this function, rewrite the function in an equivalent form:

y=x%2F%28x-5%29

y=%28%28x-5%29%2B5%29%2F%28x-5%29

y=%28x-5%29%2F%28x-5%29%2B5%2F%28x-5%29

y=1%2B5%2F%28x-5%29

For the expression 5%2F%28x-5%29...

The limit as x goes to negative infinity is 0, and the value is always negative

The limit as x goes to positive infinity is 0, and the value is always positive

The limit as x approaches 5 on the left is negative infinity

The limit as x approaches 5 on the right is positive infinity

So the range of the expression 5%2F%28x-5%29 is (-infinity,0) U (0,infinity).

And that means

ANSWER: The range of y=x%2F%28x-5%29 is (-infinity,1) U (1,infinity)

A graph....

graph%28400%2C400%2C-10%2C20%2C-10%2C5%2Cx%2F%28x-5%29%29

Answer by ikleyn(52903) About Me  (Show Source):
You can put this solution on YOUR website!
.
Find the range of y = x/(x - 5).
~~~~~~~~~~~~~~~~~~~~~~~~~~~


        Here is another solution, which does not use the conception of limits. 


The function is y = x%2F%28x-5%29.


The range of this function is the domain of the inverse function.


Let's find the inverse function.


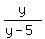For it, swap x and y in the original formula to get  x = y%2F%28y-5%29  and solve for y.


You have

    x*(y-5) = y,

    xy - 5x = y,

    xy - y = 5x,

    y*(x-1) = 5x,

    y = %285x%29%2F%281-x%29.


Thus, the domain of the inverse function  is the set of all real numbers except of x= 1.


Hence, the range of the original function is the same set of all real numbers except of x= 1.

Solved.


///////////////////////////


Comment from student :   The domain of the inverse function is the range of the given function.  Yes?


My response :   Yes.   For one-to-one functions it is always so.

The given function in this exercise is one-to-one,  so this statement is applicable to it.

It is practically the same as if you look into a mirror and see there your image . . .


Thank you for good question.


By the way, it is the kind of knowledge which everybody must have, who learns this topic and solves such problems.


Examples of one-to-one functions 

    - all linear functions  y = ax + b,  except of horizontal;

    - all monotonic polynomial functions (like y = ax^3 + const;  y = ax^5 + const and many others);

    - many trigonometric functions  y = tan(x) + const;  y = cot(x) + const  in one period domain;

    - power functions  y = 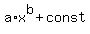a%2Ax%5Eb+%2B+const;

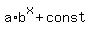    - exponential functions  y = a%2Ab%5Ex+%2B+const;

    - logarithmic functions  y = a*log(bx) + const;

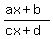    - fractional linear functions of the form  y = %28ax%2Bb%29%2F%28cx%2Bd%29;

    - and all other monotonic functions . . .