Question 1208752: Show that x^2 + 7x + 13 is prime.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Show that x^2 + 7x + 13 is prime.
~~~~~~~~~~~~~~~~~~
The precise meaning of this question is dark and unclear.
Therefore, I will re-formulate the request, to make it sensible.
Show that polynomial x^2 + 7x + 13 is a prime polynomial
in the ring of polynomials with real coefficients.
The solution is simple and beautiful, both at the same time.
Had the polynomial be non-prime (= composite) in this ring,
it would be a product of two polynomials of degree 1, i.e. linear binomials
x^2 + 7x + 13 = (ax+b)*(cx+d).
In this case, the polynomial would have real roots  and and  .
But the polynomial x^2 + 7x + 13 has a negative discriminant
d = .
But the polynomial x^2 + 7x + 13 has a negative discriminant
d =  = = 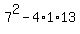 = 49 - 52 = -5.
It means that this polynomial has no real roots.
This contradiction proves that the given polynomial is a prime polynomial
in the ring of polynomials with real coefficients. = 49 - 52 = -5.
It means that this polynomial has no real roots.
This contradiction proves that the given polynomial is a prime polynomial
in the ring of polynomials with real coefficients.
Solved.
The same reasoning works for polynomials with rational coefficients or/and for
polynomials with integer coefficients.
---------------------
I don't know what is your level in Math - therefore, I fully admit that you
may understand nothing from my explanation.
Why I may think so - because the problem in your post is worded mathematically incorrectly.
On the other hand, since you brought this problem, I may assume that you have all
the necessary pre-requisites to understand my solution.
The rest depends on you - not on me.
With the full context, this problem is for the first year undergraduate university
Math student, who recently started learning Abstract Algebra.
Such a student should understand my solution adequately.
|
|
|