Question 1208740: Five workers have been hired to complete a job. If one additional worker is hired, they could complete the job 10 days earlier. If the job needs to be completed 32 days earlier, how many additional workers should be hired?
Found 4 solutions by Edwin McCravy, math_tutor2020, josgarithmetic, ikleyn:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I have edited your question to remove the dollar signs.
It seems to be a strange copy/paste error.
My method isn't as efficient compared with tutor Edwin's method, but it's another viewpoint to think about at least.
Let's say the job is moving 9000 boxes.
The number 9000 can be changed to any positive whole number and the final answer will be the same.
I'm picking this value since it's a multiple of 5 and 6.
We have these two key assumptions:
1. Each worker moves boxes at the same rate.
2. None of the workers slow down any others.
If there are 9000 boxes, and 5 workers on the job, then each person handles 9000/5 = 1800 boxes.
x = number of days to finish the job if there are 5 workers
rate*time = amount done
rate = (amount done)/time
rate = 1800/x
If there are 5 workers, each handling 1800 boxes, then each person moves 1800/x boxes per day.
This is the unit rate per worker.
..............................................
Now introduce another worker to have 5+1 = 6 workers.
Each worker now handles 9000/6 = 1500 boxes.
This extra worker brings the original number of days x to x-10 since this expanded group can complete the job 10 days earlier.
We find the unit rate per worker is 1500/(x-10) boxes per day.
Using assumption #1 mentioned earlier, we can solve 1800/x = 1500/(x-10) to get x = 60 which is the number of days it takes if you had 5 workers.
We determine that the unit rate per worker is 1800/x = 1800/60 = 30 boxes per day (or you could compute it like this 1500/(x-10) = 1500/(60-10) = 30)
Also we determine it takes x-10 = 60-10 = 50 days if you had 6 workers.
..............................................
We want the job to finish 32 days early, so we want the duration to be x-32 = 60-32 = 28 days instead of the initial 60.
n = number of extra workers you need to hire
n+5 = number of workers you'll have total when considering the initial 5
9000/(n+5) = number of boxes each worker handles
rate*time = amount done
(30 boxes per day)*(28 days) = 9000/(n+5)
30*28 = 9000/(n+5)
840 = 9000/(n+5)
840*(n+5) = 9000
840n+4200 = 9000
840n = 9000 - 4200
840n = 4800
n = 4800/840
n = 5.7142857 approximately
Note that the mixed number 5 & 5/7 is equal to 5.7142857 approximately, so this matches what Edwin got.
Obviously it's not possible to hire 0.714 of a worker, so we need to round up to n = 6. It's likely some of the workers won't have much to do as the job is getting closer to the end.
--------------------------------------------------------------------------
Answer: 6 additional workers
A similar question found here and also here
Answer by josgarithmetic(39614)   (Show Source): (Show Source):
You can put this solution on YOUR website! r, work rate of 1 worker
x, number of days work
1, number of jobs
n, how many additional workers, for the question

First two equations allows to solve for x.
and then,...
.
.
Answer by ikleyn(52756)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Five workers have been hired to complete a job. If one additional worker is hired,
they could complete the job 10 days earlier. If the job needs to be completed 32 days earlier,
how many additional workers should be hired?
~~~~~~~~~~~~~~~~~~~~~
I am 999% sure that the problem in the post is printed incorrectly and has a typo.
My interior voice tells me, and I am 99% sure that the correct formulation is THIS
Five workers have been hired to complete a job. If one additional worker is hired,
they could complete the job 10 days earlier. If the job needs to be completed  days earlier,
how many additional workers should be hired? days earlier,
how many additional workers should be hired?
I will solve the problem in this edited formulation.
SOLUTION
Let "a" be the rate of work of one worker per day.
Then the number of days for 5 workers to complete the job is  ;
the number of days for 6 workers to complete the job is ;
the number of days for 6 workers to complete the job is  .
Thus, we can write this time equation .
Thus, we can write this time equation
 - -  = 10 days. (1)
It implies = 10 days. (1)
It implies
 - -  = 10, = 10,
 = 10,
a = = 10,
a =  . (2)
+----------------------------------------------------------------+
| Thus, we found that under given condition the rate of work |
| is 1/300 of the job per day for each worker. |
+----------------------------------------------------------------+
Now we want to find the number n of additional workers (to 5 workers) to complete
the job 32 days earlier. For it, we write similar time equation to (1) . (2)
+----------------------------------------------------------------+
| Thus, we found that under given condition the rate of work |
| is 1/300 of the job per day for each worker. |
+----------------------------------------------------------------+
Now we want to find the number n of additional workers (to 5 workers) to complete
the job 32 days earlier. For it, we write similar time equation to (1)
 - -  = 30.
Substitute here a = 1/300, based on (2). You will get = 30.
Substitute here a = 1/300, based on (2). You will get
 - -  = 30.
To solve, simplify step by step. You will get
60 - = 30.
To solve, simplify step by step. You will get
60 - 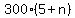 = 30,
60 - 30 = = 30,
60 - 30 =  ,
30 = ,
30 =  5 + n =
5 + n =  5 + n = 10.
n = 10 - 5 = 5.
+----------------------------------------------------------------+
| Second part of the solution can be worded in different way. |
+----------------------------------------------------------------+
We just found that the rate of work of one worker is 1/300 of the job per day.
It means that the entire job is 300 man-days.
5 workers can complete this job in 300/5 = 60 days.
We want the job be complete in 60-30 = 30 days.
For it, 300/30 = 10 workers are needed, hence, 10 - 5 = 5 workers should be added.
ANSWER. 5 workers should be hired in addition to the original 5 workers to complete the job 32 days earlier.
5 + n = 10.
n = 10 - 5 = 5.
+----------------------------------------------------------------+
| Second part of the solution can be worded in different way. |
+----------------------------------------------------------------+
We just found that the rate of work of one worker is 1/300 of the job per day.
It means that the entire job is 300 man-days.
5 workers can complete this job in 300/5 = 60 days.
We want the job be complete in 60-30 = 30 days.
For it, 300/30 = 10 workers are needed, hence, 10 - 5 = 5 workers should be added.
ANSWER. 5 workers should be hired in addition to the original 5 workers to complete the job 32 days earlier.
Solved.
|
|
|