Question 1208701: In the SuperLottery, three balls are drawn (at random, without replacement) from white balls numbered from $1$ to $10,$ and one SuperBall is drawn (at random) from red balls numbered from $11$ to $20.$ When you buy a ticket, you choose three numbers from $1$ to $10,$ and one number from $11$ to $20.$
If the numbers on your ticket match the three white balls and the red SuperBall, then you win the jackpot. (You don't need to match the white balls in order). What is the probability that you win the jackpot?
Answer by ikleyn(52824)   (Show Source):
You can put this solution on YOUR website! .
In the SuperLottery, three balls are drawn (at random, without replacement) from white balls numbered from 1 to 10,
and one SuperBall is drawn (at random) from red balls numbered from 11 to 20.
When you buy a ticket, you choose three numbers from 1 to 10, and one number from 11 to 20.
If the numbers on your ticket match the three white balls and the red SuperBall, then you win the jackpot.
(You don't need to match the white balls in order). What is the probability that you win the jackpot?
~~~~~~~~~~~~~~~~~~~~~
To solve the problem, you should clearly understand what entities you are dealing with.
On the one hand, the lottery machine produces/creates triplets of numbers written on white balls.
The numbers on the balls are from 1 to 10, and the machine takes 3 white balls
from 10 balls at random and without replacement.
Then the machine adds to this triplet a random number from 11 to 20 written on red ball.
So, the entity which the lottery machine creates is a quadruplet, which is a random triplet
of numbers from 1 to 10 without repeating, with the attached random number from 11 to 20.
It means that there are (10*9*8)*10 = 7200 physically different possible outputs/quadruplets from the lottery machine.
On the other hand, you buys a ticket, where you selecta triplet of non-repeating numbers
from 1 to 10 on your choice, and an additional number from 11 to 20.
You win the jackpot if the machine's output matches to your bought ticket.
The number of tickets that the lottery prints, distributes and sells is (10*9*8)*10 = 7200.
Of these tickets, only 6 are winning, that contain right or equivalent permutation
of 3 "white" numbers and the right "red" number.
So, among the total amount of 7200 tickets, there are 6 tickets that win the jackpot.
Hence, if you buy and have only 1 (one) ticket, the probability to win a jackpot i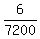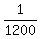s  =  . ANSWER
At this point, the solution is complete with all necessary explanations.
Solved.
|
|
|
