SOLUTION: Suppose we have a bag with $10$ slips of paper in it. Eight slips have a $7$ on them and the other two have a $9$ on them. How many $2$'s do we have to add to make the expected va

Algebra ->  Probability-and-statistics -> SOLUTION: Suppose we have a bag with $10$ slips of paper in it. Eight slips have a $7$ on them and the other two have a $9$ on them. How many $2$'s do we have to add to make the expected va      Log On


   

Question 1208670: Suppose we have a bag with $10$ slips of paper in it. Eight slips have a $7$ on them and the other two have a $9$ on them.
How many $2$'s do we have to add to make the expected value equal to $10$?
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52879) About Me  (Show Source):
You can put this solution on YOUR website!
.
Suppose we have a bag with 10 slips of paper in it. Eight slips have a 7 on them and the other two have a 9 on them.
How many 2's do we have to add to make the expected value equal to 10?
~~~~~~~~~~~~~~~ 

Whichever number of "a 2" you add, you will never get the expected value equal to 10.    ANSWER


It always will be less than 9.

Solved and answered.

One milligram of common sense is required.



Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
I'll answer the following sensible problem, which is similar in wording to
what you wrote.
Suppose we have a bag with 10 slips of paper in it. Eight slips have a 7 on them
and the other two have a 9 on them.
How many slips of paper with 2's on them do we have to add to the bag to make the
expected value of drawing one slip of paper randomly from the bag equal to 5?
Let n = the number of slips of paper that have a 2 on them we will add to the bag.
Then the number of slips of paper in the bag will be 10+n.

P(drawing a slip with a 7) = 8%2F%2810%2Bn%29, 
Expectation of the value being a 7 = expr%288%2F%2810%2Bn%29%29%2A7%22%22=%22%2256%2F%2810%2Bn%29

P(drawing a slip with a 9) = 2%2F%2810%2Bn%29, 
Expectation of the value being a 9 = expr%282%2F%2810%2Bn%29%29%2A9%22%22=%22%2218%2F%2810%2Bn%29
  
P(drawing a slip with a 2) = n%2F%2810%2Bn%29, 
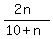Expectation of the value being a 2 = expr%28n%2F%2810%2Bn%29%29%2A2%22%22=%22%22%282n%29%2F%2810%2Bn%29

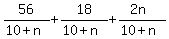
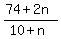Total expectation = 56%2F%2810%2Bn%29%2B18%2F%2810%2Bn%29%2B%282n%29%2F%2810%2Bn%29%22%22=%22%22%2874%2B2n%29%2F%2810%2Bn%29

Set the total expectation equal to 5:

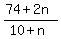
%2874%2B2n%29%2F%2810%2Bn%29%22%22=%22%225
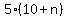
74%2B2n%22%22=%22%225%2810%2Bn%29
74%2B2n%22%22=%22%2250%2B5n
24%22%22=%22%223n
8%22%22=%22%22n

Answer:
You would need to add 8 slips of paper with 2 on them to make the
expected value of drawing one slip of paper randomly from the bag 
equal to 5.
 
[Note: you would NEVER expect to draw a slip with 5 on it because there
are none!  What "expectation" means is "what the average value of all 
umpteen slips of paper would be approximately if you could play the exact 
same game umpteen times, and averaged up your values per game over those
umpteen times you played it.]

Edwin