SOLUTION: Given an example to show that the sqrt{a^2} is not equal to a. Use it to explain why sqrt{a^2} = | a |.

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Given an example to show that the sqrt{a^2} is not equal to a. Use it to explain why sqrt{a^2} = | a |.       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1208654: Given an example to show that the sqrt{a^2} is not equal to a.
Use it to explain why sqrt{a^2} = | a |.

Answer by Shin123(626) About Me  (Show Source):
You can put this solution on YOUR website!
For an example, let's say a=-1. Then, sqrt%28a%5E2%29=sqrt%28%28-1%29%5E2%29=sqrt%281%29=1, which is not equal to -1.

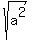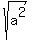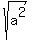Note that the square root function always takes the principal square root (the nonnegative one). If a is positive, then sqrt%28a%5E2%29 will still be a, since that is the principal square root. If a is negative, then sqrt%28a%5E2%29 will be -a, since the two square roots are a and -a, and -a is the principal square root. (a is negative, so -a is positive). If a is 0, then sqrt%28a%5E2%29 is also just a. Note that this is the exact definition of |a|. The absolute value function leaves positive numbers and zero unchanged, while taking the negative of negative numbers to make them positive. (same thing the square root function did).