Question 1208644: Royal Cruise and Carnival Cruise start at island point A. Royal sails 35 km on a bearing N 40 E to island B. Carnival sails in the direction S 30 W to island C. The distance from A to C is 70 km. How far is it from B to C?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Answer: 104.644914 km (approximate)
Explanation
Draw an xy axis.
Let's place point A at the origin (0,0).
Island B is somewhere in the northeast quadrant (aka upper right corner).
This is because notation like "N 40 E" means we face directly north and then turn 40 degrees toward the east.
Draw a segment to connect points A and B.
This segment will be the hypotenuse of a right triangle such that its vertical leg is on top of the positive y axis.
The horizontal leg is not on the x axis. Refer to the diagram shown below.
The vertical leg is labeled as dy.
The horizontal leg is labeled as dx.
The angle theta (symbol  ) is the acute angle between the hypotenuse and vertical leg.
r = hypotenuse = distance the boat travels from A to B
If you know your trig ratios, then you should realize that:
dx = r*sin(theta)
dy = r*cos(theta)
Those formulas are very useful to determine the location of island B when A = (0,0).
The dx and dy are the components of the translation vector to get from A to B.
You should find that:dx = r*sin(theta) = 35*sin(40) = 22.497566
dy = r*cos(theta) = 35*cos(40) = 26.811556 Each result is approximate. Your calculator needs to be in degree mode.
Point B is at the approximate location B = (22.497566, 26.811556) when A = (0,0).
-----------
We'll use the same idea, more or less, to figure out where point C is located on the xy grid.
Let's calculate the dx and dy values when the Carnival boat sails r = 70 kilometers and the angle mentioned is theta = 30.
We'll worry about the southwest direction later.dx = r*sin(theta) = 70*sin(30) = 35
dy = r*cos(theta) = 70*cos(30) = 60.621778 approximately Now if Carnival was sailing northeast, then we wouldn't make any adjustments to the signs of dx and dy.
However, it's instead going southwest, so we need to flip the sign of each.
The location of island C is roughly (-35, -60.621778) when A = (0,0).
I suppose you could have this rough sketch on a notecard (or have it memorized)
Or just remember to use common sense intuition when figuring out the positive or negative signs.
----------
Summary so far:
Islands B and C are at these approximate locations when A = (0,0)- B = (22.497566, 26.811556)
- C = (-35, -60.621778)
The next step from here is to use the distance formula to figure out how far it is from B to C.
Distance formula: 
I'll let the student do the scratch work.
You should get the approximate answer of 104.644914 km.
The answer will slightly vary depending how your teacher wants you to round.
I used GeoGebra to verify the answer.
Here is the specific worksheet I made for this problem. If the page is blank, then hover your mouse over any part of the box. A spiral arrow should show up. Click on it to have it refresh the page.
Answer by ikleyn(52797)  (Show Source):
You can put this solution on YOUR website! .
Consider triangle ABC.
Its side AB is 35 kilometers long..
Its side AC is 70 kilometers long.
The angle A is 50 degrees + 90 degrees + 30 degrees = 170 degrees.
To find the length of the side BC, use the cosine law
BC = 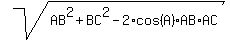 =  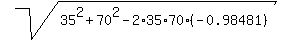= 104.645 km (rounded).
ANSWER. The distance from A to C is about 104.6 kilometers.
Solved.
|
|
|
