Question 1208637: Hello! I would appreciate it if you could help me solve this word problem:
Two candles of the same height are lit at the same time. The first is consumed in four hours, the second in three hours. Assuming that each candle burns at a constant rate, how many hours after being lit was the first candle twice the height of the second?
Found 3 solutions by Shin123, josgarithmetic, timofer:
Answer by Shin123(626)   (Show Source): (Show Source):
You can put this solution on YOUR website! Note that the exact height of the candles doesn't matter, since the candles burn at a rate proportional to their height (and the candles both have the same height). So we can assign a value to the height. To make computations easier, let the common height be 12.
For the first candle, every hour, the height decreases by 12/4=3. Therefore, after x hours, the height would be 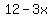 . .
For the second candle, every hour, the height decreases by 12/3=4. Therefore, after x hours, the height would be  . .
Now, we need to find the time such that the first candle had twice the height of the second. This gives us the equation  . Distributing the 2 on the right hand side gives . Distributing the 2 on the right hand side gives  Adding Adding 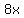 to both sides now gives to both sides now gives  . Subtracting 12 from both sides gives . Subtracting 12 from both sides gives  . Finally, dividing both sides by 5 gives . Finally, dividing both sides by 5 gives  . Therefore, the answer is . Therefore, the answer is  hours. hours.
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
Answer by timofer(106)   (Show Source): (Show Source):
|
|
|