Question 1208615: Mary and Murray travel respectively at x and y km/h heading directly towards each other across a distance of 240 km. If both start at 9 a.m. they will meet at noon. If Murray starts at 8 a.m. and Mary starts at 10 a.m. they will meet at 12:30 p.m. Find (x, y)
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
Mary and Murray travel respectively at x and y km/h heading directly towards each other across a distance of 240 km.
If both start at 9 a.m. they will meet at noon. If Murray starts at 8 a.m. and Mary starts at 10 a.m. they will meet at 12:30 p.m.
Find (x, y)
~~~~~~~~~~~~~~~~~
In the first scenario, they travel 3 hours, each.
It gives this total distance equation
3x + 3y = 240 kilometers.
In the second scenario, Mary travels 2.5 hours, Murray travels 4.5 hours.
It gives this total distance equation
2.5x + 4y = 240 kilometers.
So, we have this system of equations
3x + 3y = 240, (1)
2.5x + 4.5y = 240. (2)
To solve, from equation (1) express y = 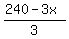 = 80-x and substitute it into equation (2).
You will get
2.5x + 4.5(80-x) = 240,
2.5x + 360 - 4.5x = 240,
2.5x - 4.5x = 240 - 360
-2x = -120,
x =  = 60.
Then y = 80-x = 80 - 60 = 20.
ANSWER. (x,y) = (60,20).
Normally, this problem is to be solved using system of two equations in two unknown.
But it can be solved MENTALLY, too, as an arithmetic word problem, without using equations,
and I will show the way to do it.
In the first scenario, Mary and Murray travel 3 hours toward each other.
Hence, their approaching rate is 240/3 = 80 kilometers per hour.
In the second scenario, Murray moves alone during 2 hours from 8 am to 10 am,
and after that, they move 2.5 hours together toward each other.
In these 2.5 hours, the distance between them decreases by 2.5*80 = 200 kilometers.
It means that the distance which Murray travels alone in 2 hours from 8:00 am to 10:am is
240-200 = 40 kilometers .
Hence, the Murray' speed is 40/2 = 20 km/h.
Then the Mary' speed is 80-20 = 60 km/h.
ANSWER. Mary' speed is 60 km/h; Murray' speed is 20 km/h.
Solved in two different ways, for your better understanding.
|
|
|
