SOLUTION: The manufacturing of semiconductor chips produces 2% defective chips. Assume the chips are independent and that a lot contains 1000 chips. Approximate the probability that between

This problem is about finding the probability for the binomial distribution.
It has very large number of trials n=1000.


Therefore, using direct formulas for binomial distribution is not recommended: it is a bad style.
Good style is to use a normal distribution as an approximation to the binomial.


This normal distribution has the mean value of m = n*p = 1000*0.02 = 20
and the standard deviation SD = 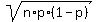 =  = 4.42719  (approximate).


Now we should estimate the area under this normal curve between X-score values  20 and 30.
Use your regular calculator TI-83/84 and its standard function normalcdf.

It calculates the cumulative probability for normal distribution.



        The pattern to use this function is  P = normalcdf ( Xmin, Xmax, mean, SD ).

                                                                              
                                               Xmin   Xmax   mean  SD              <<<---=== formatting pattern     
Thus the final probability is  P = normalcdf ( 19.5,  30.5,   20,  4.42719 ) = 0.5361.    ANSWER


Here value 19.5 is the continuity correction factor to  Xmin = 20;  value 30.5   is the continuity correction factor to  Xmax = 30.


For normalcdf, you may also use an online free of charge calculator

https://onlinestatbook.com/2/calculators/normal_dist.html