Question 1208606: Every day Jane and Bill both drive into a parking lot, and then take a subway to get to work. Jane drives 22km at 50km/h, and then takes a northbound subway that averages 30 km/h for 14 km, while Bill drives 30 km at 60 km/h and then takes a southbound subway that averages 20km/h for 6 km. It takes each of them 10 minutes to change from car to subway, and they arrive at the same destination at 8:30 a.m. At what time, to the nearest minute does the earliest of them leave home?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52770)   (Show Source):
You can put this solution on YOUR website! .
Every day Jane and Bill both drive into a parking lot, and then take a subway to get to work.
Jane drives 22km at 50km/h, and then takes a northbound subway that averages 30 km/h for 14 km, while
Bill drives 30 km at 60 km/h and then takes a southbound subway that averages 20km/h for 6 km.
It takes each of them 10 minutes to change from car to subway, and they arrive at the same destination at 8:30 a.m.
At what time, to the nearest minute does the earliest of them leave home?
~~~~~~~~~~~~~~~~~~~~~~~
Jane's travel time is  +  + 10 = 64.4 minutes (including 10 minutes for change from car to subway).
Bill's travel time is  +  + 10 = 58 minutes (including 10 minutes for change from car to subway).
(Everywhere, where you see 60 in the denominator, it is used to convert the speed from km/h to km/minute).
Jane's travel time is longer - hence, Jane leaves home earlier.
Jane leaves his home 64.4 minutes before 8:30 am, which is about 7:25 am. ANSWER
Solved.
The key for the solution is the formula t =  .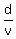
It says: to find the travel time, divide the distance by the speed.
So, we find the travel time for each part of the journey for each participant,
knowing the length of every part and the speed (which speed we convert to km/minute, for convenience).
Tutor @math_tutor2020 noticed my error in the formula, thanks for it.
So I fixed it, and now you see the corrected version.
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
Jane driving:
distance = rate*time
d = r*t
22 = 50t
t = 22/50 = 0.44 of an hour
0.44 hr = 0.44*60 = 26.4 minutes
Each decimal value is exact and hasn't been rounded.
Jane on the subway:
d = r*t
14 = 30t
t = 14/30 of an hour
That converts to (14/30)*60 = 28 minutes
Jane drives for 26.4 minutes, there's the 10 minute gap from car to subway, and then she's on the subway for 28 minutes.
Total = 26.4+10+28 = 64.4 minutes.
Round this up to 65 minutes.
If we went with 64 minutes, then we'd miss out on that extra 0.4 of a minute.
8:30 AM - 65 min
= (8 hrs + 30 min) - (60 min + 5 min)
= (8 hrs + 30 min) - (1 hr + 5 min)
= 8 hrs + 30 min - 1 hr - 5 min
= (8 hrs - 1 hr) + (30 min - 5 min)
= 7 hr + 25 min
= 7:25 AM is when Jane should leave home.
In other words, subtract off 1 hour from 8 AM to drop to 7 AM. Then we subtract the extra 5 minutes from the 30 to get 25.
Verification with WolframAlpha
--------------------------------------------------------------------------
Bill driving:
d = r*t
30 = 60t
t = 30/60 = 0.5 hr
0.5 hr = 0.5*60 = 30 min
Bill on the subway:
d = r*t
6 = 20t
t = 6/20 = 0.3 hr
0.3 hr = 0.3*60 = 18 min
Bill's total duration is 30+10+18 = 58 minutes
Tutor ikleyn has made an error in her calculation
should be
The item in red is Bill's driving speed in km/hr.
8:30 AM - 58 min
= (8 hrs + 30 min) - (60 min - 2 min)
= (8 hrs + 30 min) - (1 hr - 2 min)
= 8 hrs + 30 min - 1 hr + 2 min
= (8 hrs - 1 hr) + (30 min + 2 min)
= 7 hrs + 32 min
= 7:32 AM is when Bill should leave home
Verification with WolframAlpha
--------------------------------------------------------------------------
--------------------------------------------------------------------------
To recap,
Jane should leave home at 7:25 AM
Bill should leave home at 7:32 AM
Jane should leave 7 minutes earlier compared to bill (because 32-25 = 7).
Answer:
Jane leaves the earliest, and does so at 7:25 AM
|
|
|
