SOLUTION: 14 is added to 2\3 of a number. The result is 1 whole number 1\4 times the original number.find the numbers.

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: 14 is added to 2\3 of a number. The result is 1 whole number 1\4 times the original number.find the numbers.      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1208603: 14 is added to 2\3 of a number. The result is 1 whole number 1\4 times the original number.find the numbers.
Found 3 solutions by ikleyn, josgarithmetic, Edwin McCravy:
Answer by ikleyn(52817) About Me  (Show Source):
You can put this solution on YOUR website!
.
14 is added to 2\3 of a number. The result is 1 whole number 1\4 times the original number. find the highlight%28cross%28numbers%29%29 number.
~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

    14 + %282%2F3%29x = %285%2F4%29x.


Multiply both sides by 3*4 = 12.


    14*12 + 2*4x = 5*3x

    14*12 + 8x = 15x

    14*12 = 15x - 8x

    14*12 =    7x


Divide both sides by 7

    2*12 = x

    x = 24.    ANSWER

Solved.



Answer by josgarithmetic(39621) About Me  (Show Source):
You can put this solution on YOUR website!
You mean like,
14 is added to 2/3 of a number. The result is 1 whole number
1/4 times the original number.
find the number.
?

14%2B%282%2F3%29x.
and
14%2B2x%2F3=w%281%2F4%29x for a whole number w.
?

42%2B2x=%283%2F4%29wx
168%2B8x=3wx
3wx-8x=168
%283w-8%29x=168
x=168%2F%283w-8%29

One possibility is w=2 and x=-84

Not sure if I misunderstood.

Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
14 is added to 2\3 of a number. The result is 1 whole number 1\4 times the
original number.find the numbers.
That is not grammatical. Something is wrong or missing.

Tutor Ikleyn assumed "1 whole number 1\4" meant "1 PLUS 1/4" or 5/4.
IOW, she interpreted it to mean this:

14 is added to 2/3 of a number. The result is 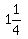1%261%2F4 times the original number. Find the number.

With her interpretation, she obtained the answer as 24.

Notice that the student wrote "find the numbers" (plural) but she 
only found only one number, and changed "numbers" to "number".

============================

Tutor josgarithmetic(39489) interpreted it as though the "1\4 times" was
reversed and should be "times 1/4".  He interpreted it as:

14 is added to 2/3 of a number. The result is 1 whole number times 1/4 the
original number. Find the numbers.  

He gave an example where the original number is -84 and the whole number is 2.
There are 6 solutions in all for his interpretation:

(-84,2), (-21,0), (6,12), (24,5), (42,4), (168,3)

============================

I will assume that the student inadvertently omitted the word PLUS.
So I'll do it with this interpretation:

14 is added to 2/3 of a number. The result is 1 whole number PLUS 1/4 times
the original number. Find the numbers.

Let x be the original number and let y be the 1 whole number.

expr%282%2F3%29x%2B14=y%2Bexpr%281%2F4%29x

Solve for y, which must be a whole number:

expr%282%2F3%29x%2B14-expr%281%2F4%29x=y 

%282%2F3-1%2F4%29x%2B14=y

%288%2F12-3%2F12%29x%2B14=y

expr%285%2F12%29x%2B14=y

Since y must be a whole number, x must be a multiple of 12
to cancel the denominator in the first term.

Let x = 12k

expr%285%2F12%29%2812k%29%2B14=y

5k%2B14=y

Whole numbers are non-negative integers, so

y=5k%2B14%3E=0

5k%3E=-14

k%3E=-14%2F5=-2.8

k is an integer, so k%3E=-2

So the infinite set of solutions is 

{ (12k, 5k+14) | k > -2 }.

Some examples of solutions are:

(-24,4), (-12,9), (0,14), (12,19), (24,24), (36,29), (48,34), ...

Edwin