SOLUTION: The area bounded by the curve 𝑦 = 𝑥^2 and the line 𝑦 = 𝑥 + 2 is rotated about the 𝑥-axis. Find the exact volume of the solid formed.

The parabola  y = x^2  and straight line  y = x+2  have two common points (x,y) = (-1,1) and  (x,y) = (2,4).

You can determine it visually by plotting equations in your graphing calculator, or by solving equation x^2 = x+2.

Also, in the interval -1 < x < 2, the line is everywhere above the parabola.

You may check/prove it from inequality x+2 > x^2.


In any case, the area bounded by these curves, is between  y= x^2 from the bottom  and  y = x+2  at the top, 
in the interval  -1 <= x <= 2.


So, this area is rotated about x-axis, and they want you find the volume of the solid body formed.


Apply the disk method.

You may consider this volume as collection of the set of disks, or, better to say, as collection of rings.

Each ring is a vertical section of the body of rotation at x = const for some value of x between -1 and 2.

Each such disk has the outer radius of  x+2  and the internal radius of  x^2, so the area of each such ring is 


     = .


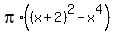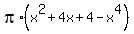To find the volume, we should integrate this expression for the area of a ring from -1 to 2.


The antiderivative is  F(x) = .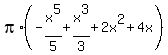


Therefore, the integral is  F(2) - F(-1).


We have F(2)  =  = ,

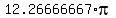        F(-1) =  = .


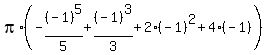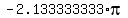Thus the integral is  F(2) - F(-1) =  = .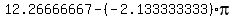


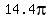ANSWER.  The volume of the solid formed is 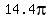  = 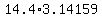 = 45.2389  (rounded).