SOLUTION: Working alone, A can complete a task in ‘a’ days and B in ‘b’ days. They take turns in doing the task with each working 2 days at a time. If A starts they finish the task i

Algebra ->  Rate-of-work-word-problems -> SOLUTION: Working alone, A can complete a task in ‘a’ days and B in ‘b’ days. They take turns in doing the task with each working 2 days at a time. If A starts they finish the task i      Log On


   

Question 1208469: Working alone, A can complete a task in ‘a’ days and B in ‘b’ days. They take turns in doing the task with each working 2 days at a time. If A starts they finish the task in exactly 10 days. If B starts, they take half a day more. How long does it take to complete the task if they both work together?

Answer by ikleyn(52756) About Me  (Show Source):
You can put this solution on YOUR website!
.
Working alone, A can complete a task in ‘a’ days and B in ‘b’ days.
They take turns in doing the task with each working 2 days at a time.
If A starts they finish the task in exactly 10 days.
If B starts, they take half a day more.
How long does it take to complete the task if they both work together?
~~~~~~~~~~~~~~~~~~~~~~ 

So, their rates of work are  1/a for A and 1/b for B.


In the first scenario, A works 6 days; B works 4 days.  So, first equation is

    6%2Fa + 4%2Fb = 1  (the entire job)         (1)


In the second scenario, A works 4.5 days; B works 6 days. So, second equation is 

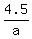    4.5%2Fa + 6%2Fb = 1  (the entire job)    (2)


To solve, multiply equation (1) by 3; multiply equation (2) by 2 and subtract the second from the first.


You will get then

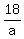    18%2Fa - 9%2Fa = 3 - 2,  or

    9%2Fa = 1.


Hence,  a = 9, which means that A makes the entire job in 9 days working alone.

Then from (1)

    4%2Fb = 1 - 6%2F9 = 1 - 2%2F3 = 1%2F3.


Hence, b = 12, which means that B makes the entire job in 12 days working alone.


Working together, they will complete the job in  

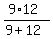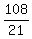    %289%2A12%29%2F%289%2B12%29 = 108%2F21 = 53%2F21 days = 51%2F7 days.    ANSWER

Solved.